Menu Close

Find-max-value-of-x-2-3xy-2y-2-subject-to-x-2-xy-y-2-1-

Tinku Tara 0 Comments
Pin




Question Number 138851 by bramlexs22 last updated on 19/Apr/21
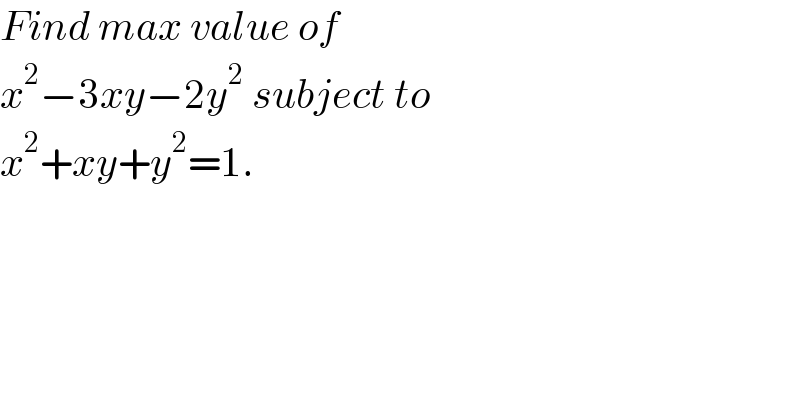
Find max value of x^2 −3xy−2y^2 subject to x^2 +xy+y^2 =1.
$${Find}\:{max}\:{value}\:{of}\: \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{xy}−\mathrm{2}{y}^{\mathrm{2}} \:{subject}\:{to}\: \\ $$$${x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} =\mathrm{1}. \\ $$
Answered by ajfour last updated on 19/Apr/21
F=x^2 −3xy−2y^2 F=x^2 +3x^2 +3y^2 −3−2y^2 F=4x^2 +y^2 −3 y=−(x/2)±(√((x^2 /4)+1−x^2 )) y=−(x/2)±(√(1−((3x^2 )/4))) F=4x^2 −2−x^2 +(x^2 /2)∓x(√(1−((3x^2 )/4))) F=((7x^2 )/2)−2∓x(√(1−((3x^2 )/4))) (dF/dx)=7x∓{(√(1−((3x^2 )/4)))−((3x^2 )/(4(√(1−((3x^2 )/4)))))}=0 ⇒ 49x^2 =1−((3x^2 )/4)+((9x^4 )/(16−12x^2 ))−((3x^2 )/2) ⇒ ((205x^2 )/4)=1+((9x^4 )/(16−12x^2 )) say x^2 =t ⇒ 205x^2 (4−3x^2 )=16−12x^2 +9x^4 ⇒ 624x^4 −832x^2 +16=0 ⇒ 39x^4 −52x^2 +1=0 x^2 =(2/3)±(√((4/9)−(1/(39)))) x^2 =(2/3)±(7/(3(√(13)))) but x^2 <(4/3) now compare F=((7x^2 )/2)−2+(√(x^2 −((3x^4 )/4))) for x^2 =0, (4/3), (2/3)±(7/(3(√(13)))) F(x^2 =0)=−2 F(x^2 =(4/3))=(8/3)≈2.6667 F(x^2 =(2/3)+(7/(3(√(13)))))≈ 2.737 F(x^2 =(2/3)−(7/(3(√(13)))))≈ −1.793 ⇒ F_(max) =F(x^2 =(2/3)+(7/(3(√(13))))) = (7/2)(((26+7(√(13)))/(39)))+{(((26+7(√(13)))/(39)))[1−(3/4)(((26+7(√(13)))/(39)))]}^(1/2) ≈ 2.737
$${F}={x}^{\mathrm{2}} −\mathrm{3}{xy}−\mathrm{2}{y}^{\mathrm{2}} \\ $$$${F}={x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} −\mathrm{3}−\mathrm{2}{y}^{\mathrm{2}} \\ $$$${F}=\mathrm{4}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{3} \\ $$$${y}=−\frac{{x}}{\mathrm{2}}\pm\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${y}=−\frac{{x}}{\mathrm{2}}\pm\sqrt{\mathrm{1}−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$${F}=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{2}−{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\mp{x}\sqrt{\mathrm{1}−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$${F}=\frac{\mathrm{7}{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}\mp{x}\sqrt{\mathrm{1}−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\frac{{dF}}{{dx}}=\mathrm{7}{x}\mp\left\{\sqrt{\mathrm{1}−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{4}}}−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{4}\sqrt{\mathrm{1}−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{4}}}}\right\}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{49}{x}^{\mathrm{2}} =\mathrm{1}−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{9}{x}^{\mathrm{4}} }{\mathrm{16}−\mathrm{12}{x}^{\mathrm{2}} }−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{\mathrm{205}{x}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{1}+\frac{\mathrm{9}{x}^{\mathrm{4}} }{\mathrm{16}−\mathrm{12}{x}^{\mathrm{2}} } \\ $$$${say}\:{x}^{\mathrm{2}} ={t} \\ $$$$\Rightarrow\:\:\mathrm{205}{x}^{\mathrm{2}} \left(\mathrm{4}−\mathrm{3}{x}^{\mathrm{2}} \right)=\mathrm{16}−\mathrm{12}{x}^{\mathrm{2}} +\mathrm{9}{x}^{\mathrm{4}} \\ $$$$\Rightarrow\:\:\mathrm{624}{x}^{\mathrm{4}} −\mathrm{832}{x}^{\mathrm{2}} +\mathrm{16}=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{39}{x}^{\mathrm{4}} −\mathrm{52}{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}\pm\sqrt{\frac{\mathrm{4}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{39}}} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}\pm\frac{\mathrm{7}}{\mathrm{3}\sqrt{\mathrm{13}}} \\ $$$${but}\:\:{x}^{\mathrm{2}} <\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${now}\:{compare} \\ $$$${F}=\frac{\mathrm{7}{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}+\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{3}{x}^{\mathrm{4}} }{\mathrm{4}}} \\ $$$${for}\:\:{x}^{\mathrm{2}} =\mathrm{0},\:\frac{\mathrm{4}}{\mathrm{3}},\:\frac{\mathrm{2}}{\mathrm{3}}\pm\frac{\mathrm{7}}{\mathrm{3}\sqrt{\mathrm{13}}} \\ $$$${F}\left({x}^{\mathrm{2}} =\mathrm{0}\right)=−\mathrm{2} \\ $$$${F}\left({x}^{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{3}}\right)=\frac{\mathrm{8}}{\mathrm{3}}\approx\mathrm{2}.\mathrm{6667} \\ $$$${F}\left({x}^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{7}}{\mathrm{3}\sqrt{\mathrm{13}}}\right)\approx\:\mathrm{2}.\mathrm{737} \\ $$$${F}\left({x}^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{7}}{\mathrm{3}\sqrt{\mathrm{13}}}\right)\approx\:−\mathrm{1}.\mathrm{793} \\ $$$$\Rightarrow\:\:{F}_{{max}} ={F}\left({x}^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{7}}{\mathrm{3}\sqrt{\mathrm{13}}}\right)\: \\ $$$$\:=\:\frac{\mathrm{7}}{\mathrm{2}}\left(\frac{\mathrm{26}+\mathrm{7}\sqrt{\mathrm{13}}}{\mathrm{39}}\right)+\left\{\left(\frac{\mathrm{26}+\mathrm{7}\sqrt{\mathrm{13}}}{\mathrm{39}}\right)\left[\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{\mathrm{26}+\mathrm{7}\sqrt{\mathrm{13}}}{\mathrm{39}}\right)\right]\right\}^{\mathrm{1}/\mathrm{2}} \\ $$$$\:\approx\:\mathrm{2}.\mathrm{737} \\ $$$$ \\ $$
Commented by ajfour last updated on 19/Apr/21
Answered by mr W last updated on 19/Apr/21
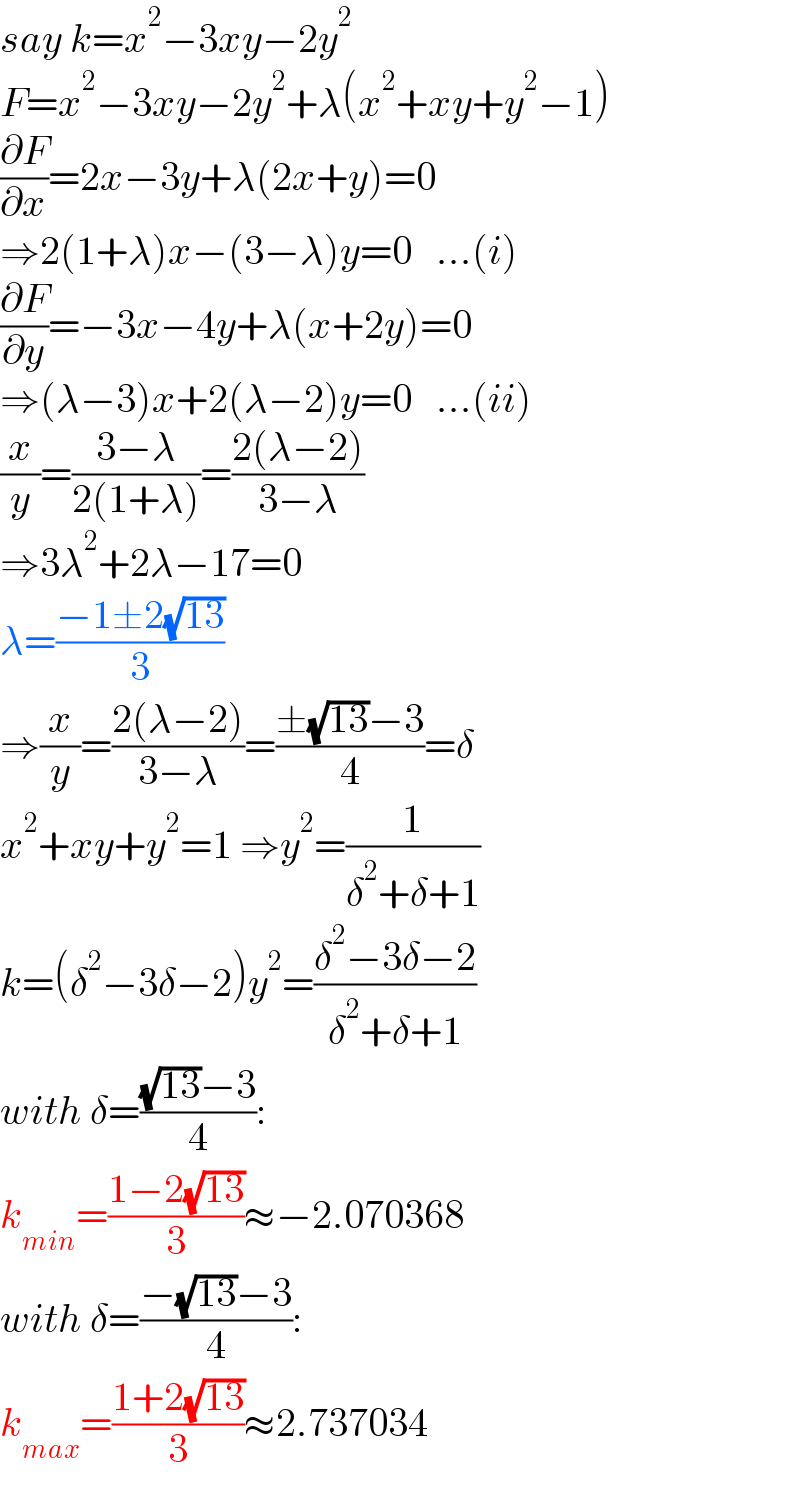
say k=x^2 −3xy−2y^2 F=x^2 −3xy−2y^2 +λ(x^2 +xy+y^2 −1) (∂F/∂x)=2x−3y+λ(2x+y)=0 ⇒2(1+λ)x−(3−λ)y=0 ...(i) (∂F/∂y)=−3x−4y+λ(x+2y)=0 ⇒(λ−3)x+2(λ−2)y=0 ...(ii) (x/y)=((3−λ)/(2(1+λ)))=((2(λ−2))/(3−λ)) ⇒3λ^2 +2λ−17=0 λ=((−1±2(√(13)))/3) ⇒(x/y)=((2(λ−2))/(3−λ))=((±(√(13))−3)/4)=δ x^2 +xy+y^2 =1 ⇒y^2 =(1/(δ^2 +δ+1)) k=(δ^2 −3δ−2)y^2 =((δ^2 −3δ−2)/(δ^2 +δ+1)) with δ=(((√(13))−3)/4): k_(min) =((1−2(√(13)))/3)≈−2.070368 with δ=((−(√(13))−3)/4): k_(max) =((1+2(√(13)))/3)≈2.737034
$${say}\:{k}={x}^{\mathrm{2}} −\mathrm{3}{xy}−\mathrm{2}{y}^{\mathrm{2}} \\ $$$${F}={x}^{\mathrm{2}} −\mathrm{3}{xy}−\mathrm{2}{y}^{\mathrm{2}} +\lambda\left({x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\frac{\partial{F}}{\partial{x}}=\mathrm{2}{x}−\mathrm{3}{y}+\lambda\left(\mathrm{2}{x}+{y}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{1}+\lambda\right){x}−\left(\mathrm{3}−\lambda\right){y}=\mathrm{0}\:\:\:…\left({i}\right) \\ $$$$\frac{\partial{F}}{\partial{y}}=−\mathrm{3}{x}−\mathrm{4}{y}+\lambda\left({x}+\mathrm{2}{y}\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\lambda−\mathrm{3}\right){x}+\mathrm{2}\left(\lambda−\mathrm{2}\right){y}=\mathrm{0}\:\:\:…\left({ii}\right) \\ $$$$\frac{{x}}{{y}}=\frac{\mathrm{3}−\lambda}{\mathrm{2}\left(\mathrm{1}+\lambda\right)}=\frac{\mathrm{2}\left(\lambda−\mathrm{2}\right)}{\mathrm{3}−\lambda} \\ $$$$\Rightarrow\mathrm{3}\lambda^{\mathrm{2}} +\mathrm{2}\lambda−\mathrm{17}=\mathrm{0} \\ $$$$\lambda=\frac{−\mathrm{1}\pm\mathrm{2}\sqrt{\mathrm{13}}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{{x}}{{y}}=\frac{\mathrm{2}\left(\lambda−\mathrm{2}\right)}{\mathrm{3}−\lambda}=\frac{\pm\sqrt{\mathrm{13}}−\mathrm{3}}{\mathrm{4}}=\delta \\ $$$${x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} =\mathrm{1}\:\Rightarrow{y}^{\mathrm{2}} =\frac{\mathrm{1}}{\delta^{\mathrm{2}} +\delta+\mathrm{1}} \\ $$$${k}=\left(\delta^{\mathrm{2}} −\mathrm{3}\delta−\mathrm{2}\right){y}^{\mathrm{2}} =\frac{\delta^{\mathrm{2}} −\mathrm{3}\delta−\mathrm{2}}{\delta^{\mathrm{2}} +\delta+\mathrm{1}} \\ $$$${with}\:\delta=\frac{\sqrt{\mathrm{13}}−\mathrm{3}}{\mathrm{4}}: \\ $$$${k}_{{min}} =\frac{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{13}}}{\mathrm{3}}\approx−\mathrm{2}.\mathrm{070368} \\ $$$${with}\:\delta=\frac{−\sqrt{\mathrm{13}}−\mathrm{3}}{\mathrm{4}}: \\ $$$${k}_{{max}} =\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{13}}}{\mathrm{3}}\approx\mathrm{2}.\mathrm{737034} \\ $$
Commented by mr W last updated on 19/Apr/21
Commented by mr W last updated on 19/Apr/21
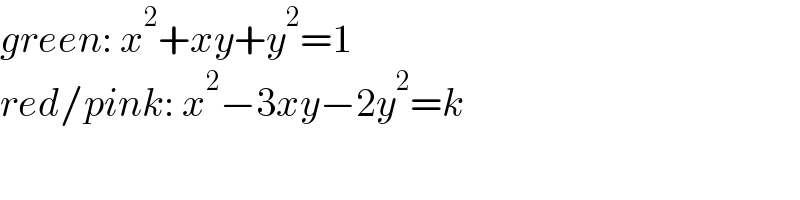
green: x^2 +xy+y^2 =1 red/pink: x^2 −3xy−2y^2 =k
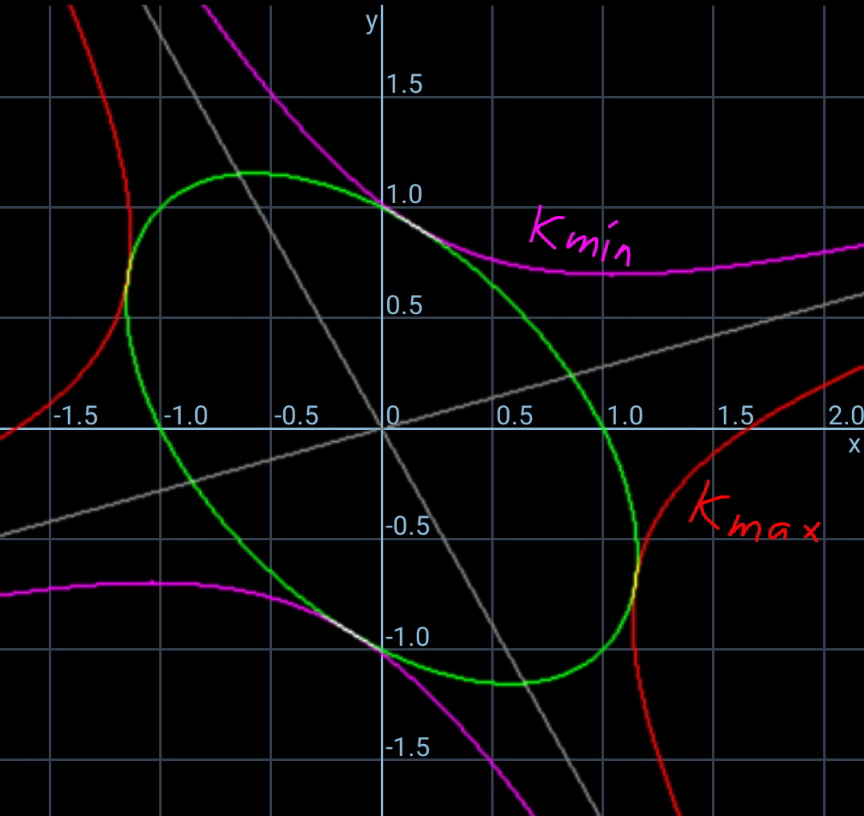
$${green}:\:{x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} =\mathrm{1} \\ $$$${red}/{pink}:\:{x}^{\mathrm{2}} −\mathrm{3}{xy}−\mathrm{2}{y}^{\mathrm{2}} ={k} \\ $$
Answered by ajfour last updated on 19/Apr/21
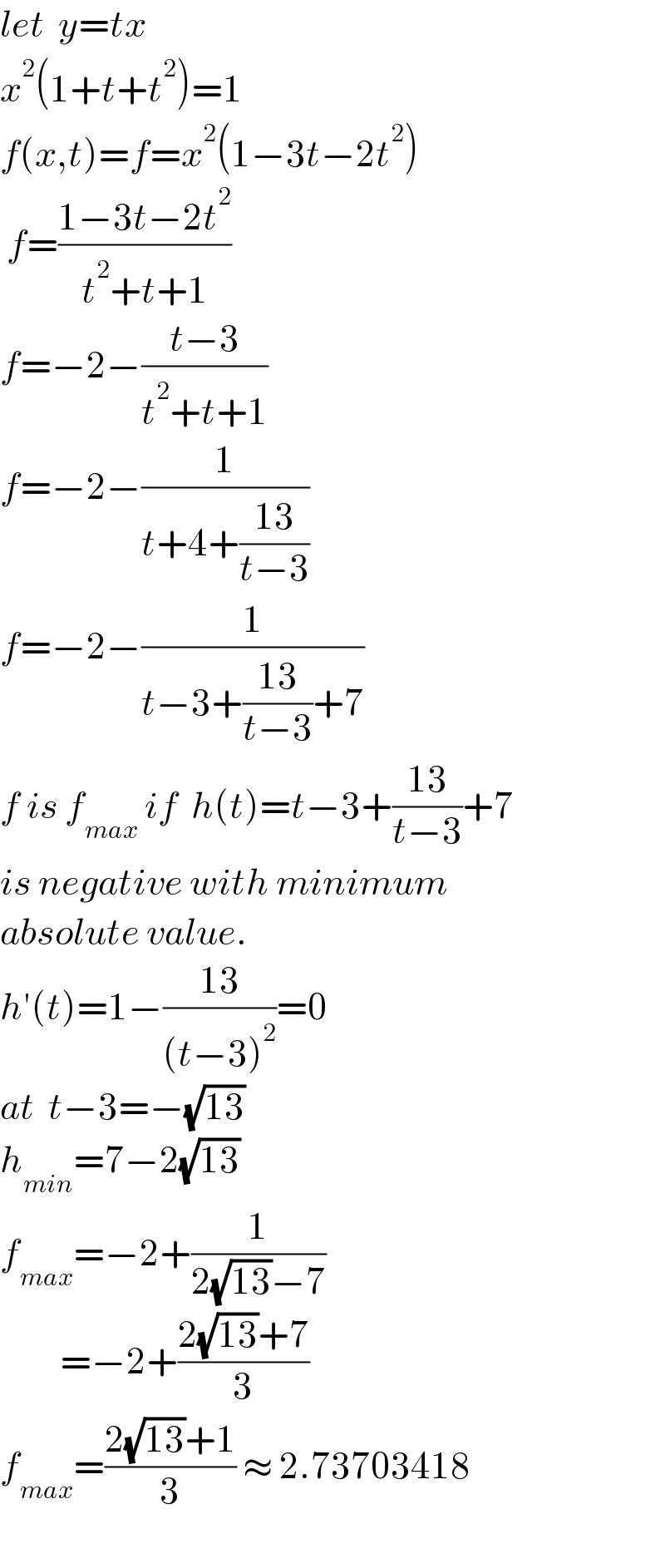
let y=tx x^2 (1+t+t^2 )=1 f(x,t)=f=x^2 (1−3t−2t^2 ) f=((1−3t−2t^2 )/(t^2 +t+1)) f=−2−((t−3)/(t^2 +t+1)) f=−2−(1/(t+4+((13)/(t−3)))) f=−2−(1/(t−3+((13)/(t−3))+7)) f is f_(max) if h(t)=t−3+((13)/(t−3))+7 is negative with minimum absolute value. h′(t)=1−((13)/((t−3)^2 ))=0 at t−3=−(√(13)) h_(min) =7−2(√(13)) f_(max) =−2+(1/(2(√(13))−7)) =−2+((2(√(13))+7)/3) f_(max) =((2(√(13))+1)/3) ≈ 2.73703418
$${let}\:\:{y}={tx} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{1}+{t}+{t}^{\mathrm{2}} \right)=\mathrm{1} \\ $$$${f}\left({x},{t}\right)={f}={x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{3}{t}−\mathrm{2}{t}^{\mathrm{2}} \right) \\ $$$$\:{f}=\frac{\mathrm{1}−\mathrm{3}{t}−\mathrm{2}{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +{t}+\mathrm{1}} \\ $$$${f}=−\mathrm{2}−\frac{{t}−\mathrm{3}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}} \\ $$$${f}=−\mathrm{2}−\frac{\mathrm{1}}{{t}+\mathrm{4}+\frac{\mathrm{13}}{{t}−\mathrm{3}}} \\ $$$${f}=−\mathrm{2}−\frac{\mathrm{1}}{{t}−\mathrm{3}+\frac{\mathrm{13}}{{t}−\mathrm{3}}+\mathrm{7}} \\ $$$${f}\:{is}\:{f}_{{max}} \:{if}\:\:{h}\left({t}\right)={t}−\mathrm{3}+\frac{\mathrm{13}}{{t}−\mathrm{3}}+\mathrm{7} \\ $$$${is}\:{negative}\:{with}\:{minimum} \\ $$$${absolute}\:{value}. \\ $$$${h}'\left({t}\right)=\mathrm{1}−\frac{\mathrm{13}}{\left({t}−\mathrm{3}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$${at}\:\:{t}−\mathrm{3}=−\sqrt{\mathrm{13}} \\ $$$${h}_{{min}} =\mathrm{7}−\mathrm{2}\sqrt{\mathrm{13}} \\ $$$${f}_{{max}} =−\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{13}}−\mathrm{7}} \\ $$$$\:\:\:\:\:\:\:\:\:=−\mathrm{2}+\frac{\mathrm{2}\sqrt{\mathrm{13}}+\mathrm{7}}{\mathrm{3}} \\ $$$${f}_{{max}} =\frac{\mathrm{2}\sqrt{\mathrm{13}}+\mathrm{1}}{\mathrm{3}}\:\approx\:\mathrm{2}.\mathrm{73703418} \\ $$$$ \\ $$
Commented by ajfour last updated on 19/Apr/21
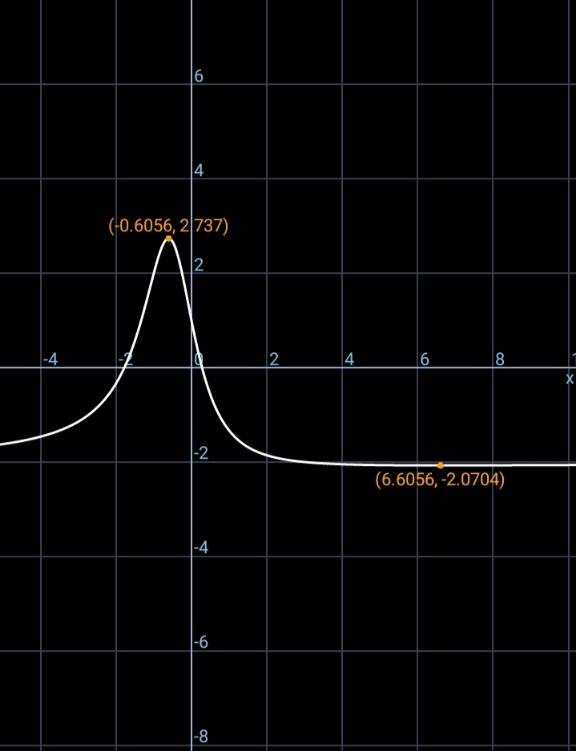
Commented by mr W last updated on 20/Apr/21
nice approach!
$${nice}\:{approach}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *