Question Number 67153 by mhmd last updated on 23/Aug/19
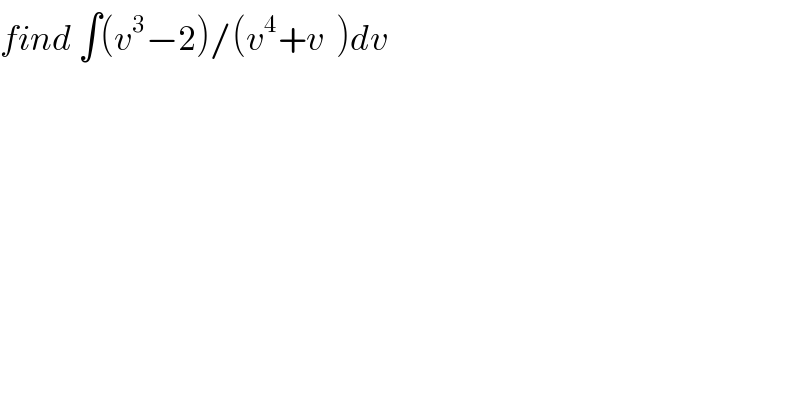
$${find}\:\int\left({v}^{\mathrm{3}} −\mathrm{2}\right)/\left({v}^{\mathrm{4}} +{v}\:\:\right){dv} \\ $$
Answered by mhmd last updated on 23/Aug/19

$$ \\ $$
Answered by MJS last updated on 23/Aug/19
![∫((v^3 −2)/(v^4 +v))dv=∫((4v^3 +1)/(4(v^4 +v)))dv−∫(9/(4(v^4 +v)))dv= ∫((4v^3 +1)/(4(v^4 +v)))dv=(1/4)∫((4v^3 +1)/(v^4 +v))dv= [t=v^4 +v → dv=(dt/(4v^3 +1))] =(1/4)∫(dt/t)=(1/4)ln t =(1/4)ln (v^4 +v) =(1/4)ln v +(1/4)ln (v^3 +1) −∫(9/(4(v^4 +v)))dv=−(9/4)∫(dv/(v^4 +v))=−(9/4)∫(dv/(v^4 (1+(1/v^3 ))))= [u=1+(1/v^3 ) → dv=−(v^4 /3)] =(3/4)∫(du/u)=(3/4)ln u =(3/4)ln (1+(1/v^3 )) =(3/4)ln (v^3 +1) −(9/4)ln v =ln (v^3 +1) −2ln v +C](https://www.tinkutara.com/question/Q67166.png)
$$\int\frac{{v}^{\mathrm{3}} −\mathrm{2}}{{v}^{\mathrm{4}} +{v}}{dv}=\int\frac{\mathrm{4}{v}^{\mathrm{3}} +\mathrm{1}}{\mathrm{4}\left({v}^{\mathrm{4}} +{v}\right)}{dv}−\int\frac{\mathrm{9}}{\mathrm{4}\left({v}^{\mathrm{4}} +{v}\right)}{dv}= \\ $$$$ \\ $$$$\:\:\:\:\:\int\frac{\mathrm{4}{v}^{\mathrm{3}} +\mathrm{1}}{\mathrm{4}\left({v}^{\mathrm{4}} +{v}\right)}{dv}=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{4}{v}^{\mathrm{3}} +\mathrm{1}}{{v}^{\mathrm{4}} +{v}}{dv}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{t}={v}^{\mathrm{4}} +{v}\:\rightarrow\:{dv}=\frac{{dt}}{\mathrm{4}{v}^{\mathrm{3}} +\mathrm{1}}\right] \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dt}}{{t}}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:{t}\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left({v}^{\mathrm{4}} +{v}\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:{v}\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left({v}^{\mathrm{3}} +\mathrm{1}\right) \\ $$$$ \\ $$$$\:\:\:\:\:−\int\frac{\mathrm{9}}{\mathrm{4}\left({v}^{\mathrm{4}} +{v}\right)}{dv}=−\frac{\mathrm{9}}{\mathrm{4}}\int\frac{{dv}}{{v}^{\mathrm{4}} +{v}}=−\frac{\mathrm{9}}{\mathrm{4}}\int\frac{{dv}}{{v}^{\mathrm{4}} \left(\mathrm{1}+\frac{\mathrm{1}}{{v}^{\mathrm{3}} }\right)}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{u}=\mathrm{1}+\frac{\mathrm{1}}{{v}^{\mathrm{3}} }\:\rightarrow\:{dv}=−\frac{{v}^{\mathrm{4}} }{\mathrm{3}}\right] \\ $$$$\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{4}}\int\frac{{du}}{{u}}=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{ln}\:{u}\:=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{v}^{\mathrm{3}} }\right)\:=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{ln}\:\left({v}^{\mathrm{3}} +\mathrm{1}\right)\:−\frac{\mathrm{9}}{\mathrm{4}}\mathrm{ln}\:{v} \\ $$$$ \\ $$$$=\mathrm{ln}\:\left({v}^{\mathrm{3}} +\mathrm{1}\right)\:−\mathrm{2ln}\:{v}\:+{C} \\ $$
