Question Number 135313 by bobhans last updated on 12/Mar/21
![Given f(x) = 5x+cos (3x) Find the value of (d/dx) [f^(−1) (1)]](https://www.tinkutara.com/question/Q135313.png)
$${Given}\:{f}\left({x}\right)\:=\:\mathrm{5}{x}+\mathrm{cos}\:\left(\mathrm{3}{x}\right) \\ $$$${Find}\:{the}\:{value}\:{of}\:\frac{{d}}{{dx}}\:\left[{f}^{−\mathrm{1}} \left(\mathrm{1}\right)\right] \\ $$
Answered by liberty last updated on 12/Mar/21
![(1)f(0)=1⇔f^(−1) (1)=0 (2) (d/dx) [ f^(−1) (1)]=(1/(5−3sin 3x)) ∣_(x = f^(−1) (1)) = (1/(5−3sin 3x))∣_(x = 0) = (1/5)](https://www.tinkutara.com/question/Q135318.png)
$$\left(\mathrm{1}\right){f}\left(\mathrm{0}\right)=\mathrm{1}\Leftrightarrow{f}^{−\mathrm{1}} \left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\frac{{d}}{{dx}}\:\left[\:{f}^{−\mathrm{1}} \left(\mathrm{1}\right)\right]=\frac{\mathrm{1}}{\mathrm{5}−\mathrm{3sin}\:\mathrm{3}{x}}\:\mid_{{x}\:=\:{f}^{−\mathrm{1}} \left(\mathrm{1}\right)} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{5}−\mathrm{3sin}\:\mathrm{3}{x}}\mid_{{x}\:=\:\mathrm{0}} \:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$
Answered by mathmax by abdo last updated on 12/Mar/21
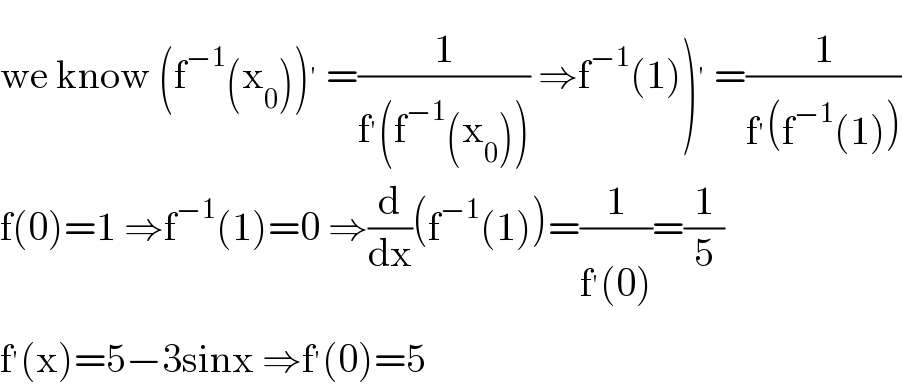
$$\left.\mathrm{we}\:\mathrm{know}\:\left(\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}_{\mathrm{0}} \right)\right)^{'} \:=\frac{\mathrm{1}}{\mathrm{f}^{'} \left(\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}_{\mathrm{0}} \right)\right)}\:\Rightarrow\mathrm{f}^{−\mathrm{1}} \left(\mathrm{1}\right)\right)^{'} \:=\frac{\mathrm{1}}{\mathrm{f}^{'} \left(\mathrm{f}^{−\mathrm{1}} \left(\mathrm{1}\right)\right)} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{1}\:\Rightarrow\mathrm{f}^{−\mathrm{1}} \left(\mathrm{1}\right)=\mathrm{0}\:\Rightarrow\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{f}^{−\mathrm{1}} \left(\mathrm{1}\right)\right)=\frac{\mathrm{1}}{\mathrm{f}^{'} \left(\mathrm{0}\right)}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)=\mathrm{5}−\mathrm{3sinx}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{0}\right)=\mathrm{5} \\ $$
