Question Number 77842 by jagoll last updated on 11/Jan/20
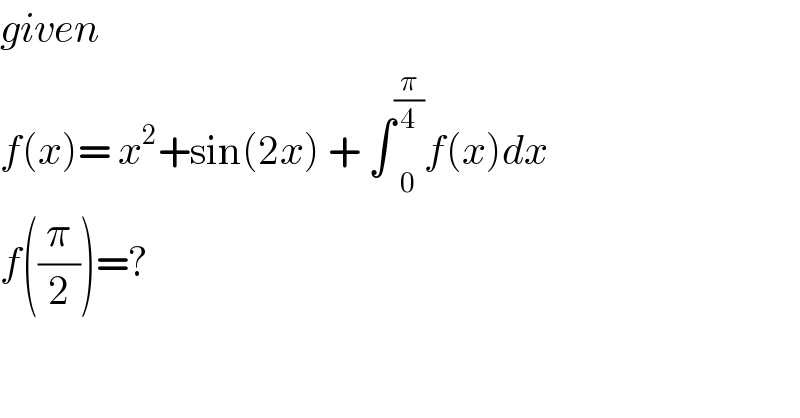
$${given}\: \\ $$$${f}\left({x}\right)=\:{x}^{\mathrm{2}} +\mathrm{sin}\left(\mathrm{2}{x}\right)\:+\:\int\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{4}}} {\:}}{f}\left({x}\right){dx} \\ $$$${f}\left(\frac{\pi}{\mathrm{2}}\right)=? \\ $$
Answered by mr W last updated on 11/Jan/20
![let ∫_0 ^(π/4) f(x)dx=a=constant f(x)= x^2 +sin(2x)+a ∫_0 ^(π/4) f(x)dx=[(x^3 /3)−((cos (2x))/2)+ax]_0 ^(π/4) =a (π^3 /(192))+(1/2)+((aπ)/4)=a ⇒a=((π^3 +96)/(48(4−π))) f(x)= x^2 +sin(2x)+((π^3 +96)/(48(4−π))) f((π/2))= (π^2 /4)+((π^3 +96)/(48(4−π)))=(((48−11π)π^2 +96)/(48(4−π)))](https://www.tinkutara.com/question/Q77844.png)
$${let}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {f}\left({x}\right){dx}={a}={constant} \\ $$$${f}\left({x}\right)=\:{x}^{\mathrm{2}} +\mathrm{sin}\left(\mathrm{2}{x}\right)+{a} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {f}\left({x}\right){dx}=\left[\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{cos}\:\left(\mathrm{2}{x}\right)}{\mathrm{2}}+{ax}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} ={a} \\ $$$$\frac{\pi^{\mathrm{3}} }{\mathrm{192}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{{a}\pi}{\mathrm{4}}={a} \\ $$$$\Rightarrow{a}=\frac{\pi^{\mathrm{3}} +\mathrm{96}}{\mathrm{48}\left(\mathrm{4}−\pi\right)} \\ $$$${f}\left({x}\right)=\:{x}^{\mathrm{2}} +\mathrm{sin}\left(\mathrm{2}{x}\right)+\frac{\pi^{\mathrm{3}} +\mathrm{96}}{\mathrm{48}\left(\mathrm{4}−\pi\right)} \\ $$$${f}\left(\frac{\pi}{\mathrm{2}}\right)=\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}}+\frac{\pi^{\mathrm{3}} +\mathrm{96}}{\mathrm{48}\left(\mathrm{4}−\pi\right)}=\frac{\left(\mathrm{48}−\mathrm{11}\pi\right)\pi^{\mathrm{2}} +\mathrm{96}}{\mathrm{48}\left(\mathrm{4}−\pi\right)} \\ $$
Commented by jagoll last updated on 11/Jan/20

$${thanks}\:{you}\:{sir} \\ $$
