Question Number 2219 by tabrez8590@gmail last updated on 09/Nov/15

$${it}\:{is}\:{necessary}\:{for}\:{diffrentiable}\:\:{function}\:{itmust}\:{becontinuty}\:{why}?{and}\:{how}\:{please}\:{explain}\:{by}\:{example} \\ $$$$ \\ $$
Answered by Filup last updated on 09/Nov/15
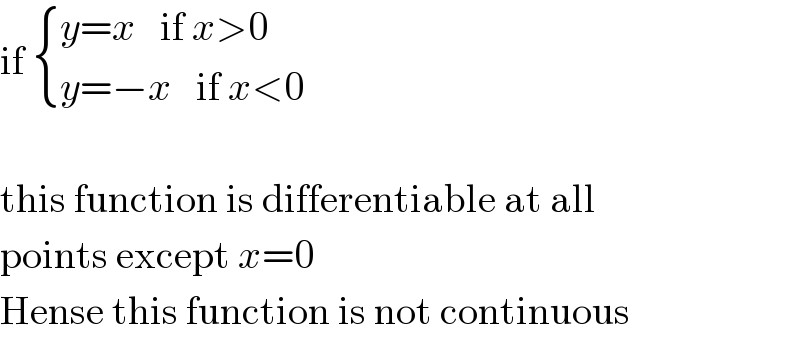
$$\mathrm{if}\:\begin{cases}{{y}={x}\:\:\:\mathrm{if}\:{x}>\mathrm{0}}\\{{y}=−{x}\:\:\:\mathrm{if}\:{x}<\mathrm{0}}\end{cases} \\ $$$$ \\ $$$$\mathrm{this}\:\mathrm{function}\:\mathrm{is}\:\mathrm{differentiable}\:\mathrm{at}\:\mathrm{all}\: \\ $$$$\mathrm{points}\:\mathrm{except}\:{x}=\mathrm{0} \\ $$$$\mathrm{Hense}\:\mathrm{this}\:\mathrm{function}\:\mathrm{is}\:\mathrm{not}\:\mathrm{continuous} \\ $$
Answered by prakash jain last updated on 09/Nov/15
![f(x)−f(x_0 )=((f(x)−f(x_0 ))/(x−x_0 ))×(x−x_0 ) lim_(x→x_0 ) [f(x)−f(x_0 )]=lim_(x→x_0 ) ((f(x)−f(x_0 ))/(x−x_0 ))×lim_(x→x_0 ) (x−x_0 ) If f(x) is differentiable at x=x_0 . Then lim_(x→x_0 ) ((f(x)−f(x_0 ))/(x−x_0 ))=f ′(x_0 ) exits. lim_(x→x_0 ) [f(x)−f(x_0 )]=f ′(x_0 )×0=0 or lim_(x→x_0 ) f(x)=f(x_0 ) Thus f(x) is continuous at x=x_0 by definition of continuity. If f(x) is differentiable at x=x_0 then it is continuous a x=x_0 .](https://www.tinkutara.com/question/Q2222.png)
$${f}\left({x}\right)−{f}\left({x}_{\mathrm{0}} \right)=\frac{{f}\left({x}\right)−{f}\left({x}_{\mathrm{0}} \right)}{{x}−{x}_{\mathrm{0}} }×\left({x}−{x}_{\mathrm{0}} \right) \\ $$$$\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}\left[{f}\left({x}\right)−{f}\left({x}_{\mathrm{0}} \right)\right]=\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}\frac{{f}\left({x}\right)−{f}\left({x}_{\mathrm{0}} \right)}{{x}−{x}_{\mathrm{0}} }×\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}\left({x}−{x}_{\mathrm{0}} \right) \\ $$$$\mathrm{If}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{differentiable}\:\mathrm{at}\:{x}={x}_{\mathrm{0}} .\:\mathrm{Then} \\ $$$$\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}\frac{{f}\left({x}\right)−{f}\left({x}_{\mathrm{0}} \right)}{{x}−{x}_{\mathrm{0}} }={f}\:'\left({x}_{\mathrm{0}} \right)\:\mathrm{exits}. \\ $$$$\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}\left[{f}\left({x}\right)−{f}\left({x}_{\mathrm{0}} \right)\right]={f}\:'\left({x}_{\mathrm{0}} \right)×\mathrm{0}=\mathrm{0} \\ $$$${or}\:\underset{{x}\rightarrow{x}_{\mathrm{0}} } {\mathrm{lim}}{f}\left({x}\right)={f}\left({x}_{\mathrm{0}} \right) \\ $$$$\mathrm{Thus}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{continuous}\:\mathrm{at}\:{x}={x}_{\mathrm{0}} \:\mathrm{by}\:\mathrm{definition} \\ $$$$\mathrm{of}\:\mathrm{continuity}. \\ $$$$\mathrm{If}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{differentiable}\:\mathrm{at}\:{x}={x}_{\mathrm{0}} \:\mathrm{then}\:\mathrm{it}\:\mathrm{is} \\ $$$$\mathrm{continuous}\:\mathrm{a}\:{x}={x}_{\mathrm{0}} . \\ $$
