Question Number 135820 by Ar Brandon last updated on 16/Mar/21
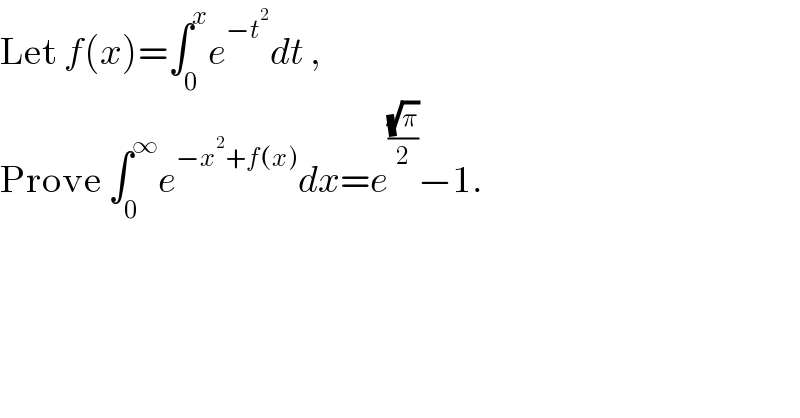
$$\mathrm{Let}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} {e}^{−{t}^{\mathrm{2}} } {dt}\:, \\ $$$$\mathrm{Prove}\:\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} +{f}\left({x}\right)} {dx}={e}^{\frac{\sqrt{\pi}}{\mathrm{2}}} −\mathrm{1}. \\ $$
Answered by mindispower last updated on 19/Mar/21
![∫_0 ^∞ e^(−x^2 +f(x)) dx f′(x)=e^(−x^2 ) ⇔∫_0 ^∞ f′(x)e^(f(x)) dx=[e^(f(x)) ]_0 ^∞ =e^(∫_0 ^∞ e^(−t^2 ) dt) −1 =e^(√(π/4)) −1=e^((√π)/2) −1](https://www.tinkutara.com/question/Q136215.png)
$$\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} +{f}\left({x}\right)} {dx} \\ $$$${f}'\left({x}\right)={e}^{−{x}^{\mathrm{2}} } \\ $$$$\Leftrightarrow\int_{\mathrm{0}} ^{\infty} {f}'\left({x}\right){e}^{{f}\left({x}\right)} {dx}=\left[{e}^{{f}\left({x}\right)} \right]_{\mathrm{0}} ^{\infty} ={e}^{\int_{\mathrm{0}} ^{\infty} {e}^{−{t}^{\mathrm{2}} } {dt}} −\mathrm{1} \\ $$$$={e}^{\sqrt{\frac{\pi}{\mathrm{4}}}} −\mathrm{1}={e}^{\frac{\sqrt{\pi}}{\mathrm{2}}} −\mathrm{1} \\ $$$$ \\ $$
