let-f-x-tanx-tan2x-Find-the-points-of-discontinuity-of-f-on-0-2pi-and-determine-wether-each-duscontinuity-is-a-point-discontinuity-a-jump-discontinuity-or-a-vertical-asymtote-

Question Number 73569 by Rio Michael last updated on 13/Nov/19

$${let}\:{f}\left({x}\right)\:=\:\frac{{tanx}}{{tan}\mathrm{2}{x}}\:.\:{Find}\:{the}\:{points}\:{of}\:{discontinuity} \\ $$$${of}\:{f}\:{on}\:\left[\mathrm{0},\mathrm{2}\pi\right]\:{and}\:{determine}\:{wether}\:{each}\:{duscontinuity}\:{is} \\ $$$${a}\:{point}\:{discontinuity},{a}\:{jump}\:{discontinuity},{or}\:{a}\:{vertical}\:{asymtote} \\ $$$$ \\ $$

Commented by Rio Michael last updated on 13/Nov/19

$${i}\:{appreciate} \\ $$

Commented by kaivan.ahmadi last updated on 13/Nov/19

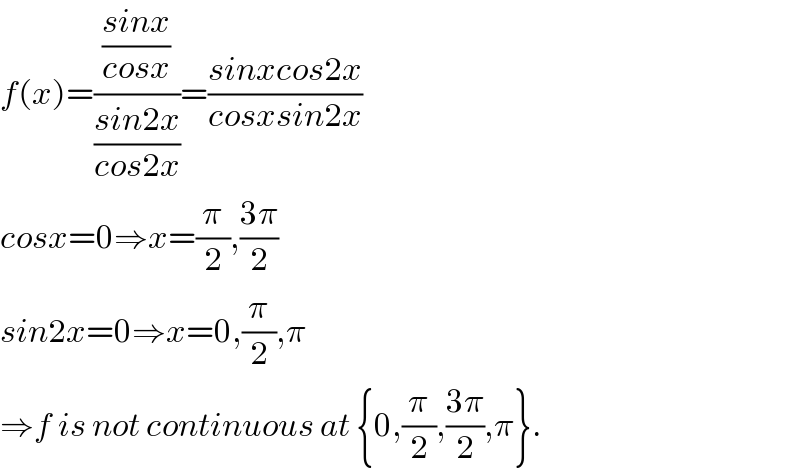
$${f}\left({x}\right)=\frac{\frac{{sinx}}{{cosx}}}{\frac{{sin}\mathrm{2}{x}}{{cos}\mathrm{2}{x}}}=\frac{{sinxcos}\mathrm{2}{x}}{{cosxsin}\mathrm{2}{x}} \\ $$$${cosx}=\mathrm{0}\Rightarrow{x}=\frac{\pi}{\mathrm{2}},\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$$${sin}\mathrm{2}{x}=\mathrm{0}\Rightarrow{x}=\mathrm{0},\frac{\pi}{\mathrm{2}},\pi \\ $$$$\Rightarrow{f}\:{is}\:{not}\:{continuous}\:{at}\:\left\{\mathrm{0},\frac{\pi}{\mathrm{2}},\frac{\mathrm{3}\pi}{\mathrm{2}},\pi\right\}. \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com