Question Number 66816 by mathmax by abdo last updated on 20/Aug/19
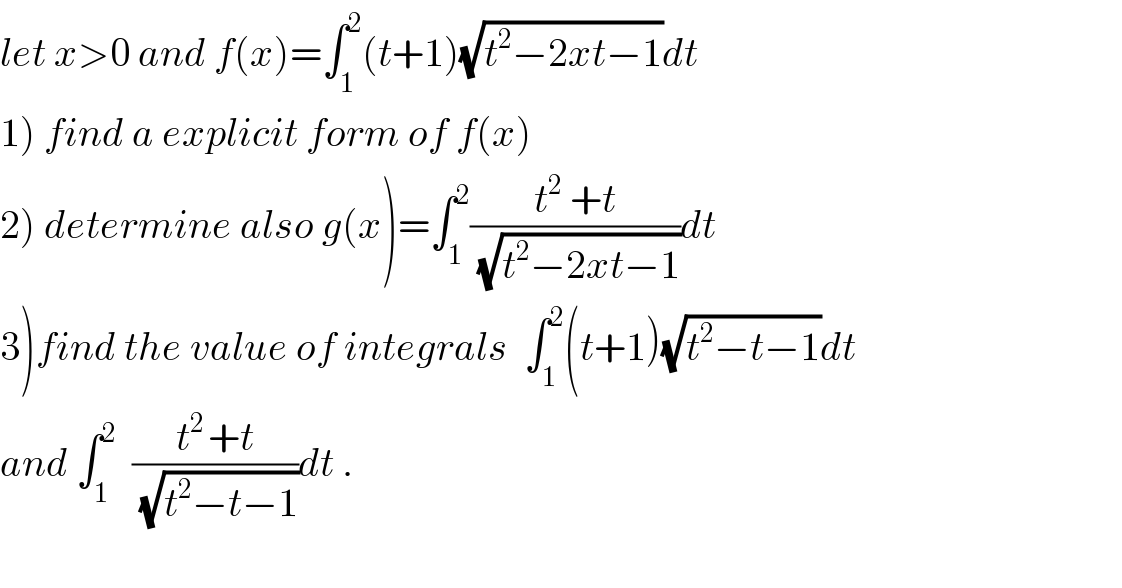
$${let}\:{x}>\mathrm{0}\:{and}\:{f}\left({x}\right)=\int_{\mathrm{1}} ^{\mathrm{2}} \left({t}+\mathrm{1}\right)\sqrt{{t}^{\mathrm{2}} −\mathrm{2}{xt}−\mathrm{1}}{dt} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{determine}\:{also}\:{g}\left({x}\right)=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{t}^{\mathrm{2}} \:+{t}}{\:\sqrt{{t}^{\mathrm{2}} −\mathrm{2}{xt}−\mathrm{1}}}{dt} \\ $$$$\left.\mathrm{3}\right){find}\:{the}\:{value}\:{of}\:{integrals}\:\:\int_{\mathrm{1}} ^{\mathrm{2}} \left({t}+\mathrm{1}\right)\sqrt{{t}^{\mathrm{2}} −{t}−\mathrm{1}}{dt} \\ $$$${and}\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\frac{{t}^{\mathrm{2}\:} +{t}}{\:\sqrt{{t}^{\mathrm{2}} −{t}−\mathrm{1}}}{dt}\:. \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 23/Aug/19
![1) we have f(x)=∫_1 ^2 (t+1)(√(t^2 −2xt−1))dt we have t^2 −2xt−1 =t^2 −2xt+x^2 −x^2 −1 =(t−x)^2 −((√(1+x^2 )))^2 we do the changement t−x =(√(1+x^2 ))ch(u) ⇒ f(x) =∫_(argch(((1−x)/( (√(1+x^2 )))))) ^(arch(((2−x)/( (√(1+x^2 )))))) (x+(√(1+x^2 ))ch(u))(√(1+x^2 ))sh(u)du =x(√(1+x^2 )) ∫_(argch(((1−x)/( (√(1+x^2 )))))) ^(argch(((2−x)/( (√(1+x^2 )))))) sh(u)du +(1+x^2 )∫_(argch(((1−x)/( (√(1+x^2 )))))) ^(argch(((2−x)/( (√(1+x^2 )))))) ch(u)sh(u)du we have ∫_(argch(((1−x)/( (√(1+x^2 )))))) ^(argch(((2−x)/( (√(1+x^2 )))))) sh(u)du =[ch(u)]_(arg(...)) ^(arg(...)) argch(((2−x)/( (√(1+x^2 ))))) =ln(((2−x)/( (√(1+x^2 ))))+(√(1+(((2−x)^2 )/(1+x^2 ))))) argch(((1−x)/( (√(1+x^2 )))))=ln(((1−x)/( (√(1+x^2 ))))+(√(1+(((1−x)^2 )/(1+x^2 ))))) ⇒ ∫_(argch(((1−x)/( (√(1+x^2 )))))) ^(argch(((2−x)/( (√(1+x^2 )))))) sh(u)du =(1/2)[ e^u −e^(−u) ]..=(1/2){((2−x)/( (√(1+x^2 ))))+(√(1+(((2−x)^2 )/(1+x^2 )))) −(1/((((2−x)/( (√(1+x^2 )))) +(√(1+(((2−x)^2 )/(1+x^2 )))))^2 ))−(((1−x)/( (√(1+x^2 ))))+(√(1+(((1−x)^2 )/(1+x^2 ))))) +(1/((1−x)/( (√(1+x^2 )))))+(√(1+(((1−x)^2 )/(1+x^2 )))). ∫_(α(x)) ^(β(x)) ch(u)sh(u)du =(1/2)∫_(α(x)) ^(β(x)) sh(2u)du =(1/4)[ch(2u)]_(α(x)) ^(β(x)) =(1/8)[ e^(2u) −e^(−2u) ]_(α(x)) ^(β(x)) =(1/8)[e^(2β(x)) −e^(−2β(x)) −e^(2α(x) ) +e^(−2α(x)) ] wit α(x)=argch(((1−x)/( (√(1+x^2 ))))) and β(x) =argch(((2−x)/( (√(1+x^2 ))))) the value of f(x) is known...](https://www.tinkutara.com/question/Q67159.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({x}\right)=\int_{\mathrm{1}} ^{\mathrm{2}} \left({t}+\mathrm{1}\right)\sqrt{{t}^{\mathrm{2}} −\mathrm{2}{xt}−\mathrm{1}}{dt}\:\:\:{we}\:{have} \\ $$$${t}^{\mathrm{2}} −\mathrm{2}{xt}−\mathrm{1}\:={t}^{\mathrm{2}} −\mathrm{2}{xt}+{x}^{\mathrm{2}} −{x}^{\mathrm{2}} −\mathrm{1}\:=\left({t}−{x}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$${we}\:{do}\:{the}\:{changement}\:{t}−{x}\:=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{ch}\left({u}\right)\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\int_{{argch}\left(\frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)} ^{{arch}\left(\frac{\mathrm{2}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)} \:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{ch}\left({u}\right)\right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{sh}\left({u}\right){du} \\ $$$$={x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\int_{{argch}\left(\frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)} ^{{argch}\left(\frac{\mathrm{2}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)} {sh}\left({u}\right){du}\:\:\:+\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\int_{{argch}\left(\frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)} ^{{argch}\left(\frac{\mathrm{2}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)} {ch}\left({u}\right){sh}\left({u}\right){du} \\ $$$${we}\:{have}\:\int_{{argch}\left(\frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)} ^{{argch}\left(\frac{\mathrm{2}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)} {sh}\left({u}\right){du}\:=\left[{ch}\left({u}\right)\right]_{{arg}\left(…\right)} ^{{arg}\left(…\right)} \\ $$$${argch}\left(\frac{\mathrm{2}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)\:={ln}\left(\frac{\mathrm{2}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}+\sqrt{\mathrm{1}+\frac{\left(\mathrm{2}−{x}\right)^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }}\right) \\ $$$${argch}\left(\frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)={ln}\left(\frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}+\sqrt{\mathrm{1}+\frac{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }}\right)\:\Rightarrow \\ $$$$\int_{{argch}\left(\frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)} ^{{argch}\left(\frac{\mathrm{2}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)} \:{sh}\left({u}\right){du}\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\:{e}^{{u}} −{e}^{−{u}} \right]..=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{2}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}+\sqrt{\mathrm{1}+\frac{\left(\mathrm{2}−{x}\right)^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }}\right. \\ $$$$−\frac{\mathrm{1}}{\left(\frac{\mathrm{2}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:+\sqrt{\mathrm{1}+\frac{\left(\mathrm{2}−{x}\right)^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }}\right)^{\mathrm{2}} }−\left(\frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}+\sqrt{\mathrm{1}+\frac{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }}\right) \\ $$$$+\frac{\mathrm{1}}{\frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}}+\sqrt{\mathrm{1}+\frac{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }}. \\ $$$$\int_{\alpha\left({x}\right)} ^{\beta\left({x}\right)} \:{ch}\left({u}\right){sh}\left({u}\right){du}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\alpha\left({x}\right)} ^{\beta\left({x}\right)} {sh}\left(\mathrm{2}{u}\right){du}\:=\frac{\mathrm{1}}{\mathrm{4}}\left[{ch}\left(\mathrm{2}{u}\right)\right]_{\alpha\left({x}\right)} ^{\beta\left({x}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left[\:{e}^{\mathrm{2}{u}} \:−{e}^{−\mathrm{2}{u}} \right]_{\alpha\left({x}\right)} ^{\beta\left({x}\right)} \:=\frac{\mathrm{1}}{\mathrm{8}}\left[{e}^{\mathrm{2}\beta\left({x}\right)} −{e}^{−\mathrm{2}\beta\left({x}\right)} −{e}^{\mathrm{2}\alpha\left({x}\right)\:} \:+{e}^{−\mathrm{2}\alpha\left({x}\right)} \right] \\ $$$${wit}\:\alpha\left({x}\right)={argch}\left(\frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)\:{and}\:\beta\left({x}\right)\:={argch}\left(\frac{\mathrm{2}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right) \\ $$$${the}\:{value}\:{of}\:{f}\left({x}\right)\:{is}\:{known}… \\ $$
Commented by mathmax by abdo last updated on 23/Aug/19
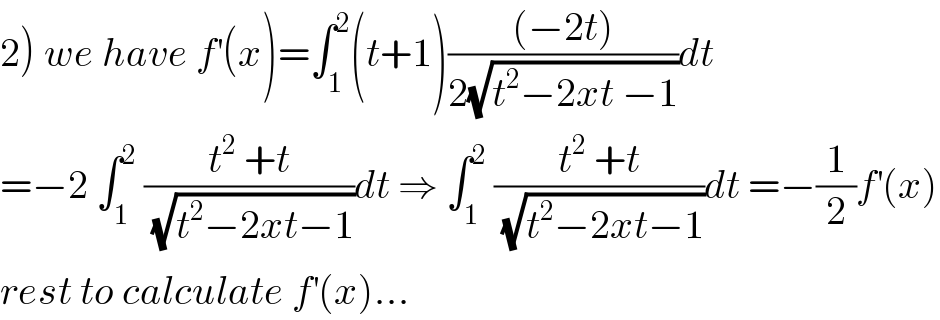
$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}^{'} \left({x}\right)=\int_{\mathrm{1}} ^{\mathrm{2}} \left({t}+\mathrm{1}\right)\frac{\left(−\mathrm{2}{t}\right)}{\mathrm{2}\sqrt{{t}^{\mathrm{2}} −\mathrm{2}{xt}\:−\mathrm{1}}}{dt} \\ $$$$=−\mathrm{2}\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{{t}^{\mathrm{2}} \:+{t}}{\:\sqrt{{t}^{\mathrm{2}} −\mathrm{2}{xt}−\mathrm{1}}}{dt}\:\Rightarrow\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{{t}^{\mathrm{2}} \:+{t}}{\:\sqrt{{t}^{\mathrm{2}} −\mathrm{2}{xt}−\mathrm{1}}}{dt}\:=−\frac{\mathrm{1}}{\mathrm{2}}{f}^{'} \left({x}\right) \\ $$$${rest}\:{to}\:{calculate}\:{f}^{'} \left({x}\right)… \\ $$
Commented by mathmax by abdo last updated on 23/Aug/19
![3) let I =∫_1 ^2 (t+1)(√(t^2 −t−1))dt we have t^2 −t−1= t^2 −2(t/2) +(1/4)−1−(1/4) =(t−(1/2))^2 −(5/4) we do the changement t−(1/2) =((√5)/2) ch(u) ⇒u=argch(((2t−1)/( (√5)))) ⇒ I =∫_(argch((1/( (√5))))) ^(argch((3/( (√5))))) ((1/2)+((√5)/2)ch(u))((√5)/2)sh(u)du =((√5)/4)∫_(ln((1/( (√5)))+(√(1+(1/5))))) ^(ln((3/( (√5)))+(√(1+(9/5))))) sh(u)du +(5/8) ∫_(ln((1/( (√5)))+(√(1+(1/5))))) ^(ln((3/( (√5)))+(√(1+(9/5))))) sh(2u) du =((√5)/8)[ e^u −e^(−u) ]_(ln((1/( (√5)))+((√6)/( (√5))))) ^(ln((3/( (√5)))+((√(13))/( (√5))))) +(5/(16))[ e^(2u) −e^(−2u) ]_(ln(((1+(√6))/( (√5))))) ^(ln(((3+(√(13)))/( (√5))))) =((√5)/8){ ((3+(√(13)))/( (√5))) −(1/((3+(√(13)))/( (√5)))) −(((1+(√6))/( (√5))))+(1/((1+(√6))/( (√5))))} +(5/(16)){ (((3+(√(13)))/( (√5))))^2 −(1/((((3+(√(13)))/( (√5))))^2 ))−(((1+(√6))/( (√5))))^2 +(1/((((1+(√6))/( (√5))))^2 ))}](https://www.tinkutara.com/question/Q67161.png)
$$\left.\mathrm{3}\right)\:{let}\:{I}\:=\int_{\mathrm{1}} ^{\mathrm{2}} \left({t}+\mathrm{1}\right)\sqrt{{t}^{\mathrm{2}} −{t}−\mathrm{1}}{dt}\:\:\:\:{we}\:{have}\:{t}^{\mathrm{2}} −{t}−\mathrm{1}= \\ $$$${t}^{\mathrm{2}} −\mathrm{2}\frac{{t}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\:=\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:−\frac{\mathrm{5}}{\mathrm{4}}\:\:{we}\:{do}\:{the}\:{changement} \\ $$$${t}−\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\:{ch}\left({u}\right)\:\Rightarrow{u}={argch}\left(\frac{\mathrm{2}{t}−\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)\:\Rightarrow \\ $$$${I}\:=\int_{{argch}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)} ^{{argch}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\right)} \:\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}{ch}\left({u}\right)\right)\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}{sh}\left({u}\right){du} \\ $$$$=\frac{\sqrt{\mathrm{5}}}{\mathrm{4}}\int_{{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}}}\right)} ^{{ln}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}+\sqrt{\mathrm{1}+\frac{\mathrm{9}}{\mathrm{5}}}\right)} \:\:{sh}\left({u}\right){du}\:+\frac{\mathrm{5}}{\mathrm{8}}\:\int_{{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}}}\right)} ^{{ln}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}+\sqrt{\mathrm{1}+\frac{\mathrm{9}}{\mathrm{5}}}\right)} \:{sh}\left(\mathrm{2}{u}\right)\:{du} \\ $$$$=\frac{\sqrt{\mathrm{5}}}{\mathrm{8}}\left[\:{e}^{{u}} −{e}^{−{u}} \right]_{{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}+\frac{\sqrt{\mathrm{6}}}{\:\sqrt{\mathrm{5}}}\right)} ^{{ln}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}+\frac{\sqrt{\mathrm{13}}}{\:\sqrt{\mathrm{5}}}\right)} \:\:+\frac{\mathrm{5}}{\mathrm{16}}\left[\:{e}^{\mathrm{2}{u}} \:−{e}^{−\mathrm{2}{u}} \right]_{{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{6}}}{\:\sqrt{\mathrm{5}}}\right)} ^{{ln}\left(\frac{\mathrm{3}+\sqrt{\mathrm{13}}}{\:\sqrt{\mathrm{5}}}\right)} \\ $$$$=\frac{\sqrt{\mathrm{5}}}{\mathrm{8}}\left\{\:\frac{\mathrm{3}+\sqrt{\mathrm{13}}}{\:\sqrt{\mathrm{5}}}\:−\frac{\mathrm{1}}{\frac{\mathrm{3}+\sqrt{\mathrm{13}}}{\:\sqrt{\mathrm{5}}}}\:−\left(\frac{\mathrm{1}+\sqrt{\mathrm{6}}}{\:\sqrt{\mathrm{5}}}\right)+\frac{\mathrm{1}}{\frac{\mathrm{1}+\sqrt{\mathrm{6}}}{\:\sqrt{\mathrm{5}}}}\right\} \\ $$$$+\frac{\mathrm{5}}{\mathrm{16}}\left\{\:\:\left(\frac{\mathrm{3}+\sqrt{\mathrm{13}}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\left(\frac{\mathrm{3}+\sqrt{\mathrm{13}}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} }−\left(\frac{\mathrm{1}+\sqrt{\mathrm{6}}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\left(\frac{\mathrm{1}+\sqrt{\mathrm{6}}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} }\right\} \\ $$
