Question Number 891 by 123456 last updated on 17/Apr/15
![lets f:[0,1]→R lets e_n :[0,1]→R lets a_n :[0,1]→R such that f(x)=Σ_(i=1) ^3 a_i (x)e_i (x) ∫_0 ^1 e_i (x)e_j (x)dx= { (1,(i=j)),(0,(i≠j)) :} so ∫_0 ^1 [f(x)]^2 dx=?](https://www.tinkutara.com/question/Q891.png)
$$\mathrm{lets}\:{f}:\left[\mathrm{0},\mathrm{1}\right]\rightarrow\mathbb{R} \\ $$$$\mathrm{lets}\:{e}_{{n}} :\left[\mathrm{0},\mathrm{1}\right]\rightarrow\mathbb{R} \\ $$$$\mathrm{lets}\:{a}_{{n}} :\left[\mathrm{0},\mathrm{1}\right]\rightarrow\mathbb{R} \\ $$$$\mathrm{such}\:\mathrm{that} \\ $$$${f}\left({x}\right)=\underset{{i}=\mathrm{1}} {\overset{\mathrm{3}} {\sum}}{a}_{{i}} \left({x}\right){e}_{{i}} \left({x}\right) \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{e}_{{i}} \left({x}\right){e}_{{j}} \left({x}\right){dx}=\begin{cases}{\mathrm{1}}&{{i}={j}}\\{\mathrm{0}}&{{i}\neq{j}}\end{cases} \\ $$$$\mathrm{so} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left[{f}\left({x}\right)\right]^{\mathrm{2}} {dx}=? \\ $$
Commented by prakash jain last updated on 16/Apr/15
![[f(x)]^2 =a_1 ^2 e_1 ^2 +a_2 ^2 e_2 ^2 +a_3 ^2 e_3 ^2 +2a_1 e_1 a_2 e_2 +2a_1 e_1 a_3 e_3 +2a_2 e_2 a_3 e_3 I think the given input is insufficient.](https://www.tinkutara.com/question/Q899.png)
$$\left[{f}\left({x}\right)\right]^{\mathrm{2}} ={a}_{\mathrm{1}} ^{\mathrm{2}} {e}_{\mathrm{1}} ^{\mathrm{2}} +{a}_{\mathrm{2}} ^{\mathrm{2}} {e}_{\mathrm{2}} ^{\mathrm{2}} +{a}_{\mathrm{3}} ^{\mathrm{2}} {e}_{\mathrm{3}} ^{\mathrm{2}} +\mathrm{2}{a}_{\mathrm{1}} {e}_{\mathrm{1}} {a}_{\mathrm{2}} {e}_{\mathrm{2}} +\mathrm{2}{a}_{\mathrm{1}} {e}_{\mathrm{1}} {a}_{\mathrm{3}} {e}_{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}{a}_{\mathrm{2}} {e}_{\mathrm{2}} {a}_{\mathrm{3}} {e}_{\mathrm{3}} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{given}\:\mathrm{input}\:\mathrm{is}\:\mathrm{insufficient}. \\ $$
Commented by 123456 last updated on 17/Apr/15
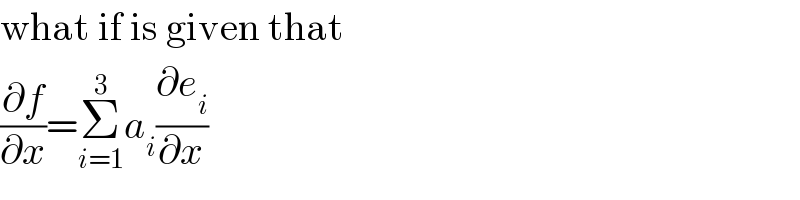
$$\mathrm{what}\:\mathrm{if}\:\mathrm{is}\:\mathrm{given}\:\mathrm{that} \\ $$$$\frac{\partial{f}}{\partial{x}}=\underset{{i}=\mathrm{1}} {\overset{\mathrm{3}} {\sum}}{a}_{{i}} \frac{\partial{e}_{{i}} }{\partial{x}} \\ $$
Answered by prakash jain last updated on 17/Apr/15
![Given (∂f/∂x)=Σ_(i=1) ^3 a_i (∂e_i /∂x) ∫_0 ^1 [f(x)]^2 dx=Σ_(i=1) ^3 a_i ^2 ∫_0 ^1 e_1 ^2 dx =Σ_(i=1) ^3 a_i ^2](https://www.tinkutara.com/question/Q903.png)
$$\mathrm{Given}\:\frac{\partial{f}}{\partial{x}}=\underset{{i}=\mathrm{1}} {\overset{\mathrm{3}} {\sum}}{a}_{{i}} \frac{\partial{e}_{{i}} }{\partial{x}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left[{f}\left({x}\right)\right]^{\mathrm{2}} {dx}=\underset{{i}=\mathrm{1}} {\overset{\mathrm{3}} {\sum}}{a}_{{i}} ^{\mathrm{2}} \int_{\mathrm{0}} ^{\mathrm{1}} {e}_{\mathrm{1}} ^{\mathrm{2}} {dx} \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{\mathrm{3}} {\sum}}{a}_{{i}} ^{\mathrm{2}} \\ $$
