Question Number 135190 by liberty last updated on 11/Mar/21
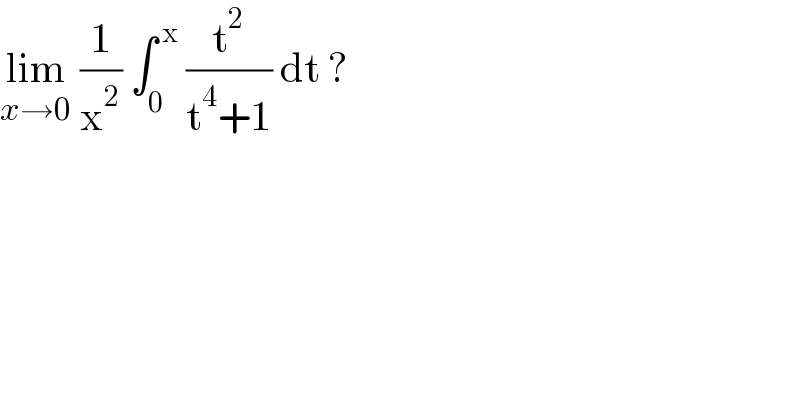
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\:\mathrm{x}} \:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}\:\mathrm{dt}\:? \\ $$$$ \\ $$
Answered by metamorfose last updated on 11/Mar/21
![∃c∈[0,x] , (1/x^2 )∫_0 ^x (t^2 /((t^4 +1)))dt=(c^2 /(x(c^4 +1))) ∀c∈[0,x] , 0≤c^2 ≤x^2 ... so : 0≤(c^2 /(x(c^4 +1)))≤(x/(c^4 +1)) thus : lim_(x→0) (c^2 /(x(c^4 +1)))=0 lim_(x→0) (1/x^2 )∫_0 ^x (t^2 /(t^4 +1))dt=0 ...](https://www.tinkutara.com/question/Q135198.png)
$$\exists{c}\in\left[\mathrm{0},{x}\right]\:,\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\int_{\mathrm{0}} ^{{x}} \frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{4}} +\mathrm{1}\right)}{dt}=\frac{{c}^{\mathrm{2}} }{{x}\left({c}^{\mathrm{4}} +\mathrm{1}\right)} \\ $$$$\forall{c}\in\left[\mathrm{0},{x}\right]\:,\:\mathrm{0}\leqslant{c}^{\mathrm{2}} \leqslant{x}^{\mathrm{2}} \:…\:{so}\:: \\ $$$$\mathrm{0}\leqslant\frac{{c}^{\mathrm{2}} }{{x}\left({c}^{\mathrm{4}} +\mathrm{1}\right)}\leqslant\frac{{x}}{{c}^{\mathrm{4}} +\mathrm{1}}\:{thus}\::\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{c}^{\mathrm{2}} }{{x}\left({c}^{\mathrm{4}} +\mathrm{1}\right)}=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\int_{\mathrm{0}} ^{{x}} \frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} +\mathrm{1}}{dt}=\mathrm{0}\:… \\ $$
Answered by benjo_mathlover last updated on 11/Mar/21
![lim_(x→0) ((∫_0 ^( x) (t^2 /(t^4 +1)) dt)/x^2 ) [ L′Ho^� pital ] = lim_(x→0) ((x^2 /(x^4 +1))/(2x)) = lim_(x→0) (x/(2(x^4 +1)))= 0](https://www.tinkutara.com/question/Q135202.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\int_{\mathrm{0}} ^{\:\mathrm{x}} \frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}\:\mathrm{dt}}{\mathrm{x}^{\mathrm{2}} }\:\left[\:\mathrm{L}'\mathrm{H}\hat {\mathrm{o}pital}\:\right] \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}}{\mathrm{2x}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}}{\mathrm{2}\left(\mathrm{x}^{\mathrm{4}} +\mathrm{1}\right)}=\:\mathrm{0} \\ $$
