Question Number 140050 by mnjuly1970 last updated on 03/May/21
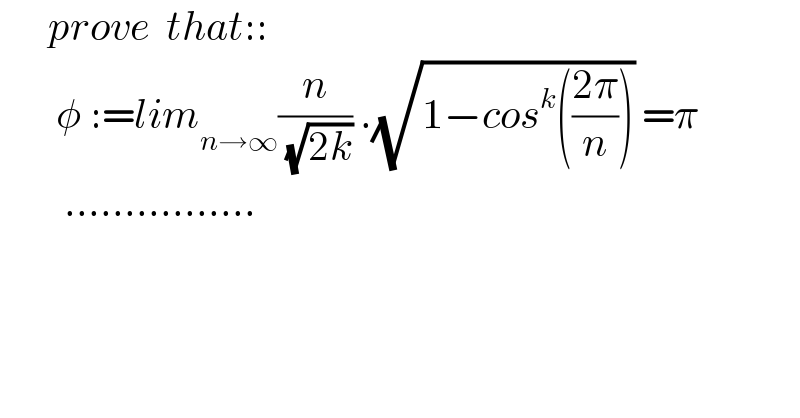
$$\:\:\:\:\:\:{prove}\:\:{that}:: \\ $$$$\:\:\:\:\:\:\:\phi\::={lim}_{{n}\rightarrow\infty} \frac{{n}}{\:\sqrt{\mathrm{2}{k}}}\:.\sqrt{\mathrm{1}−{cos}^{{k}} \left(\frac{\mathrm{2}\pi}{{n}}\right)}\:=\pi \\ $$$$\:\:\:\:\:\:\:\:……………. \\ $$$$ \\ $$
Answered by Kamel last updated on 04/May/21

Answered by Dwaipayan Shikari last updated on 03/May/21

$$\frac{{n}}{\:\sqrt{\mathrm{2}{k}}}\sqrt{\mathrm{1}−{cos}^{{k}} \left(\frac{\mathrm{2}\pi}{{n}}\right)}\approx\mathrm{2}\frac{{n}}{\:\sqrt{\mathrm{2}{k}}}\sqrt{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{2}\pi^{\mathrm{2}} {k}}{\mathrm{2}!{n}^{\mathrm{2}} }\right)}=\frac{\sqrt{\mathrm{2}}{n}\pi}{\:\sqrt{\mathrm{2}{k}}}.\frac{\sqrt{{k}}}{{n}}=\pi \\ $$
Answered by mnjuly1970 last updated on 04/May/21
![prove::............. (1/n) =t −⇒{_( t→0^+ ) ^( n→∞) φ:= lim_(t→0^+ ) (1/( (√(2k)))) ((1/t))(√(1−cos^k (2πt))) :=lim_(t→0^+ ) (1/( (√(2k)))) ((1/t)){(√(1−cos(2πt))) .(√(1+cos(2πt)+...+cos^(k−1) (2πt))) :=lim_(t→0^+ ) (1/( (√(2k))))((1/t)){(√(2sin^2 (πt))) .(√(1+cos(πt)+...+cos^(k−1) (2πt))) } :=lim_(t→0^+ ) (((√2) sin(πt))/( (√2) (√k))) (√([1+1+1+....+1]:=k times)) ........ φ : = π .......](https://www.tinkutara.com/question/Q140088.png)
$$\:\:\:\:\:\:\:\:\:\:\:{prove}::…………. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{n}}\:={t}\:−\Rightarrow\left\{_{\:{t}\rightarrow\mathrm{0}^{+} } ^{\:{n}\rightarrow\infty} \:\right. \\ $$$$\:\:\:\:\:\:\:\phi:=\:{lim}_{{t}\rightarrow\mathrm{0}^{+} } \frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{k}}}\:\left(\frac{\mathrm{1}}{{t}}\right)\sqrt{\mathrm{1}−{cos}^{{k}} \left(\mathrm{2}\pi{t}\right)}\: \\ $$$$\:\:\:\:\:\:\:\::={lim}_{{t}\rightarrow\mathrm{0}^{+} } \frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{k}}}\:\left(\frac{\mathrm{1}}{{t}}\right)\left\{\sqrt{\mathrm{1}−{cos}\left(\mathrm{2}\pi{t}\right)}\:.\sqrt{\mathrm{1}+{cos}\left(\mathrm{2}\pi{t}\right)+…+{cos}^{{k}−\mathrm{1}} \left(\mathrm{2}\pi{t}\right)}\:\right. \\ $$$$\:\:\:\:\:\:\:\:\::={lim}_{{t}\rightarrow\mathrm{0}^{+} } \frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{k}}}\left(\frac{\mathrm{1}}{{t}}\right)\left\{\sqrt{\mathrm{2}{sin}^{\mathrm{2}} \left(\pi{t}\right)}\:.\sqrt{\mathrm{1}+{cos}\left(\pi{t}\right)+…+{cos}^{{k}−\mathrm{1}} \left(\mathrm{2}\pi{t}\right)}\:\right\} \\ $$$$\:\:\:\:\:\:\:\:\::={lim}_{{t}\rightarrow\mathrm{0}^{+} } \frac{\sqrt{\mathrm{2}}\:{sin}\left(\pi{t}\right)}{\:\sqrt{\mathrm{2}}\:\sqrt{{k}}}\:\sqrt{\left[\mathrm{1}+\mathrm{1}+\mathrm{1}+….+\mathrm{1}\right]:={k}\:\:{times}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……..\:\:\phi\::\:=\:\pi\:……. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$
