Question Number 137112 by Algoritm last updated on 29/Mar/21
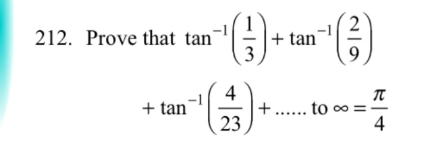
Answered by Ñï= last updated on 03/Apr/21
![tan^(−1) ((1/3))+tan^(−1) ((2/9))+tan^(−1) ((4/(23)))+... =arg(3+i)+arg(9+2i)+arg(23+4i)+... =arg[(3+i)(9+2i)(23+4i)∙...] =arg[(25+15i)(23+4i)∙...] =arg[(515+445i)∙...] =arg(x+iy) =tan^(−1) (y/x)](https://www.tinkutara.com/question/Q137492.png)
$$\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{9}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{23}}\right)+… \\ $$$$={arg}\left(\mathrm{3}+{i}\right)+{arg}\left(\mathrm{9}+\mathrm{2}{i}\right)+{arg}\left(\mathrm{23}+\mathrm{4}{i}\right)+… \\ $$$$={arg}\left[\left(\mathrm{3}+{i}\right)\left(\mathrm{9}+\mathrm{2}{i}\right)\left(\mathrm{23}+\mathrm{4}{i}\right)\centerdot…\right] \\ $$$$={arg}\left[\left(\mathrm{25}+\mathrm{15}{i}\right)\left(\mathrm{23}+\mathrm{4}{i}\right)\centerdot…\right] \\ $$$$={arg}\left[\left(\mathrm{515}+\mathrm{445}{i}\right)\centerdot…\right] \\ $$$$={arg}\left({x}+{iy}\right) \\ $$$$=\mathrm{tan}^{−\mathrm{1}} \frac{{y}}{{x}} \\ $$
