Question Number 138330 by JulioCesar last updated on 12/Apr/21

Answered by Dwaipayan Shikari last updated on 12/Apr/21
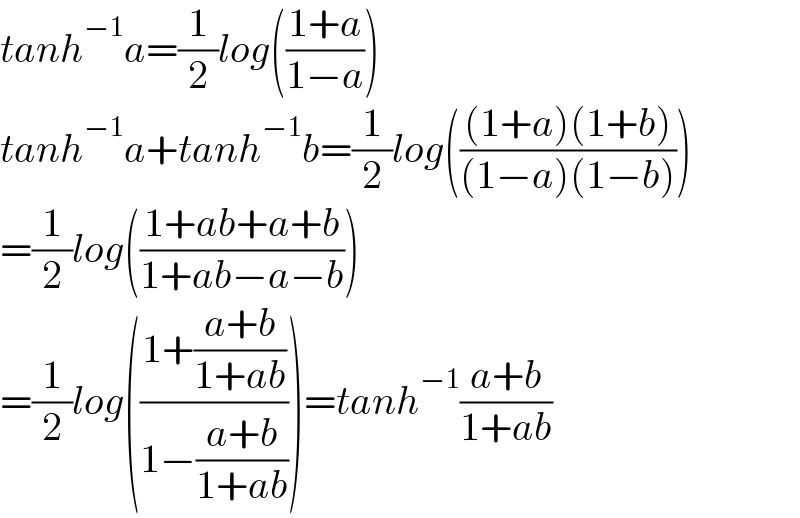
$${tanh}^{−\mathrm{1}} {a}=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}\right) \\ $$$${tanh}^{−\mathrm{1}} {a}+{tanh}^{−\mathrm{1}} {b}=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\left(\mathrm{1}+{a}\right)\left(\mathrm{1}+{b}\right)}{\left(\mathrm{1}−{a}\right)\left(\mathrm{1}−{b}\right)}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\mathrm{1}+{ab}+{a}+{b}}{\mathrm{1}+{ab}−{a}−{b}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\mathrm{1}+\frac{{a}+{b}}{\mathrm{1}+{ab}}}{\mathrm{1}−\frac{{a}+{b}}{\mathrm{1}+{ab}}}\right)={tanh}^{−\mathrm{1}} \frac{{a}+{b}}{\mathrm{1}+{ab}} \\ $$
Commented by JulioCesar last updated on 12/Apr/21

$${Thank}\:{sir}! \\ $$
Answered by Ankushkumarparcha last updated on 12/Apr/21
![Solution: let tanh^(−1) (a) = x & tanh^(−1) (b) = y Consider LHS = tanh^(−1) (a)+tanh^(−1) (b) & RHS = tanh^(−1) (((a+b)/(1+ab))) Solving RHS i.e, tanh^(−1) (((a+b)/(1+ab))) = tanh^(−1) (((((e^x −e^(−x) )/(e^x +e^(−x) )) + ((e^y −e^(−y) )/(e^y +e^(−y) )))/(1+(((e^x −e^(−x) )/(e^x +e^(−x) )))(((e^y −e^(−y) )/(e^y +e^(−y) )))))) RHS = tanh^(−1) (((e^(x+y) +e^(x−y) −e^(y−x) −e^(−x−y) +e^(x+y) −e^(x−y) +e^(y−x) −e^(−x−y) )/(e^(x+y) +e^(x−y) +e^(y−x) +e^(−x−y) +e^(x+y) −e^(x−y) −e^(y−x) +e^(−x−y) ))) RHS = tanh^(−1) (((e^(x+y) −e^(−x−y) )/(e^(x+y) +e^(−x−y) ))) => tanh^(−1) [tanh(x+y)] RHS = x+y = tanh^(−1) (a)+tanh^(−1) (b) =LHS ( #Hence proved)](https://www.tinkutara.com/question/Q138344.png)
$${Solution}:\:{let}\:\mathrm{tanh}^{−\mathrm{1}} \left({a}\right)\:=\:{x}\:\:\&\:\:\mathrm{tanh}^{−\mathrm{1}} \left({b}\right)\:=\:{y} \\ $$$${Consider}\:{LHS}\:=\:\mathrm{tanh}^{−\mathrm{1}} \left({a}\right)+\mathrm{tanh}^{−\mathrm{1}} \left({b}\right)\:\:\&\:\:{RHS}\:=\:\mathrm{tanh}^{−\mathrm{1}} \left(\frac{{a}+{b}}{\mathrm{1}+{ab}}\right) \\ $$$${Solving}\:{RHS}\:\:{i}.{e},\:\mathrm{tanh}^{−\mathrm{1}} \left(\frac{{a}+{b}}{\mathrm{1}+{ab}}\right)\:=\:\mathrm{tanh}^{−\mathrm{1}} \left(\frac{\frac{{e}^{{x}} −{e}^{−{x}} }{{e}^{{x}} +{e}^{−{x}} }\:+\:\frac{{e}^{{y}} −{e}^{−{y}} }{{e}^{{y}} +{e}^{−{y}} }}{\mathrm{1}+\left(\frac{{e}^{{x}} −{e}^{−{x}} }{{e}^{{x}} +{e}^{−{x}} }\right)\left(\frac{{e}^{{y}} −{e}^{−{y}} }{{e}^{{y}} +{e}^{−{y}} }\right)}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${RHS}\:=\:\mathrm{tanh}^{−\mathrm{1}} \left(\frac{{e}^{{x}+{y}} +{e}^{{x}−{y}} −{e}^{{y}−{x}} −{e}^{−{x}−{y}} +{e}^{{x}+{y}} −{e}^{{x}−{y}} +{e}^{{y}−{x}} −{e}^{−{x}−{y}} }{{e}^{{x}+{y}} +{e}^{{x}−{y}} +{e}^{{y}−{x}} +{e}^{−{x}−{y}} +{e}^{{x}+{y}} −{e}^{{x}−{y}} −{e}^{{y}−{x}} +{e}^{−{x}−{y}} }\right) \\ $$$${RHS}\:=\:\mathrm{tanh}^{−\mathrm{1}} \left(\frac{{e}^{{x}+{y}} −{e}^{−{x}−{y}} }{{e}^{{x}+{y}} +{e}^{−{x}−{y}} }\right)\:=>\:\mathrm{tanh}^{−\mathrm{1}} \left[\mathrm{tanh}\left({x}+{y}\right)\right] \\ $$$${RHS}\:=\:{x}+{y}\:=\:\mathrm{tanh}^{−\mathrm{1}} \left({a}\right)+\mathrm{tanh}^{−\mathrm{1}} \left({b}\right)\:={LHS}\:\:\left(\:#{Hence}\:{proved}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by JulioCesar last updated on 12/Apr/21

$${Thank}\:{sir}! \\ $$
