Question Number 142475 by cherokeesay last updated on 01/Jun/21

Answered by qaz last updated on 01/Jun/21
![f((1/x))+x^2 f(x)=0 ⇒f(x)+(1/x^2 )f((1/x))=0 I=∫_(1/x) ^x f(t)dt=∫_x ^(1/x) f((1/t))(−(1/t^2 ))dt=∫_(1/x) ^x f((1/t))(dt/t^2 ) =(1/2)∫_(1/x) ^x [f(t)+f((1/t))(1/t^2 )]dt=0](https://www.tinkutara.com/question/Q142478.png)
$$\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{x}^{\mathrm{2}} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{0} \\ $$$$\mathrm{I}=\int_{\frac{\mathrm{1}}{\mathrm{x}}} ^{\mathrm{x}} \mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}=\int_{\mathrm{x}} ^{\frac{\mathrm{1}}{\mathrm{x}}} \mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{t}}\right)\left(−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right)\mathrm{dt}=\int_{\frac{\mathrm{1}}{\mathrm{x}}} ^{\mathrm{x}} \mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{t}}\right)\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\mathrm{1}}{\mathrm{x}}} ^{\mathrm{x}} \left[\mathrm{f}\left(\mathrm{t}\right)+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{t}}\right)\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right]\mathrm{dt}=\mathrm{0} \\ $$
Commented by cherokeesay last updated on 01/Jun/21

$${thank}\:{you}\:{sir}. \\ $$
Answered by mathmax by abdo last updated on 01/Jun/21
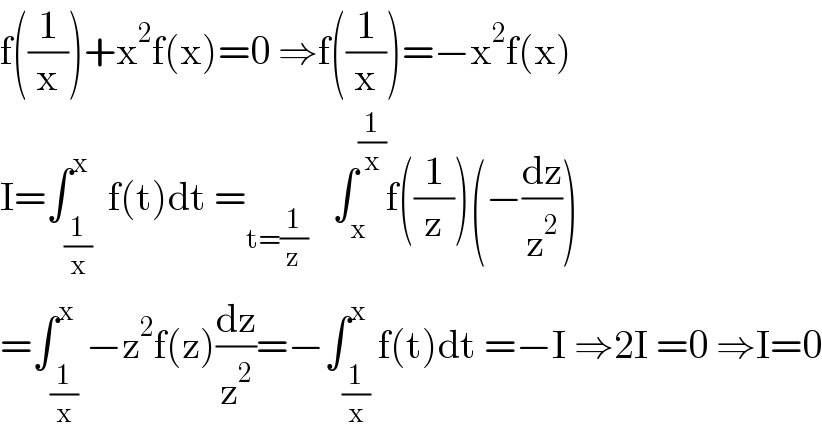
$$\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{x}^{\mathrm{2}} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{0}\:\Rightarrow\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=−\mathrm{x}^{\mathrm{2}} \mathrm{f}\left(\mathrm{x}\right)\: \\ $$$$\mathrm{I}=\int_{\frac{\mathrm{1}}{\mathrm{x}}} ^{\mathrm{x}} \:\mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}\:=_{\mathrm{t}=\frac{\mathrm{1}}{\mathrm{z}}} \:\:\:\int_{\mathrm{x}} ^{\frac{\mathrm{1}}{\mathrm{x}}} \mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{z}}\right)\left(−\frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{2}} }\right) \\ $$$$=\int_{\frac{\mathrm{1}}{\mathrm{x}}} ^{\mathrm{x}} −\mathrm{z}^{\mathrm{2}} \mathrm{f}\left(\mathrm{z}\right)\frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{2}} }=−\int_{\frac{\mathrm{1}}{\mathrm{x}}} ^{\mathrm{x}} \mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}\:=−\mathrm{I}\:\Rightarrow\mathrm{2I}\:=\mathrm{0}\:\Rightarrow\mathrm{I}=\mathrm{0} \\ $$
