Question-1479

Question Number 1479 by yyy last updated on 12/Aug/15

$$ \\ $$$$ \\ $$

Answered by 123456 last updated on 12/Aug/15

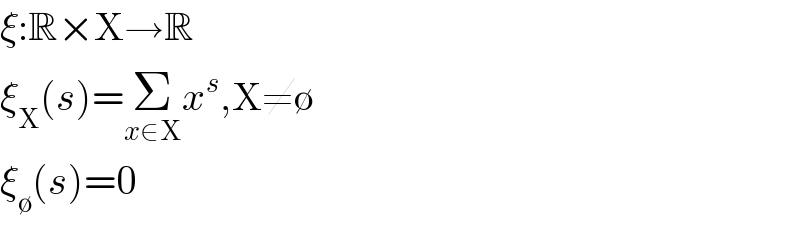
ξ:R×X→R ξ_X (s)=Σ_(x∈X) x^s ,X≠∅ ξ_∅ (s)=0

$$\xi:\mathbb{R}×\mathrm{X}\rightarrow\mathbb{R} \\ $$$$\xi_{\mathrm{X}} \left({s}\right)=\underset{{x}\in\mathrm{X}} {\sum}{x}^{{s}} ,\mathrm{X}\neq\emptyset \\ $$$$\xi_{\emptyset} \left({s}\right)=\mathrm{0} \\ $$

Answered by 123456 last updated on 17/Aug/15

200 [b,a,g,g,qm,b,m,c,d,p][s,c] [1,1,5,1,2,5,4,14,20,25][2,5] A_1 [4b,20a,4m,32b] [4 ,20 ,16 ,160] A_2 [2b,20a,2m,30b][4c] [2 ,20 ,8 ,140][20] T_1 [6b,24a,16g,4qm,12m,1c] [6 ,24 ,100 ,8 ,48 ,14]

$$\mathrm{200} \\ $$$$\left[\mathrm{b},\mathrm{a},\mathrm{g},\mathrm{g},\mathrm{qm},\mathrm{b},\mathrm{m},\mathrm{c},\mathrm{d},\mathrm{p}\right]\left[\mathrm{s},\mathrm{c}\right] \\ $$$$\left[\mathrm{1},\mathrm{1},\mathrm{5},\mathrm{1},\mathrm{2},\mathrm{5},\mathrm{4},\mathrm{14},\mathrm{20},\mathrm{25}\right]\left[\mathrm{2},\mathrm{5}\right] \\ $$$$\mathrm{A}_{\mathrm{1}} \left[\mathrm{4b},\mathrm{20a},\mathrm{4m},\mathrm{32b}\right] \\ $$$$\:\:\:\:\:\:\left[\mathrm{4}\:\:,\mathrm{20}\:\:\:,\mathrm{16}\:\:,\mathrm{160}\right] \\ $$$$\mathrm{A}_{\mathrm{2}} \left[\mathrm{2b},\mathrm{20a},\mathrm{2m},\mathrm{30b}\right]\left[\mathrm{4c}\right] \\ $$$$\:\:\:\:\:\:\left[\mathrm{2}\:\:,\mathrm{20}\:\:\:,\mathrm{8}\:\:\:\:,\mathrm{140}\right]\left[\mathrm{20}\right] \\ $$$$\mathrm{T}_{\mathrm{1}} \left[\mathrm{6b},\mathrm{24a},\mathrm{16g},\mathrm{4qm},\mathrm{12m},\mathrm{1c}\right] \\ $$$$\:\:\:\:\:\:\left[\mathrm{6}\:\:,\mathrm{24}\:\:,\mathrm{100}\:,\mathrm{8}\:\:\:\:\:\:,\mathrm{48}\:\:\:\:,\mathrm{14}\right] \\ $$

Answered by 123456 last updated on 26/Aug/15

1000×1000^(2n−1) =1000000^n 10^3 ×(10^3 )^(2n−1) =(10^6 )^n 10^3 ×10^(6n−3) =10^(6n) 10^(3+6n−3) =10^(6n) 10^(6n) =10^(6n) a_n =2n−1 {(1,1),(2,3),(3,5),(4,7),(5,9),...}

$$\mathrm{1000}×\mathrm{1000}^{\mathrm{2}{n}−\mathrm{1}} =\mathrm{1000000}^{{n}} \\ $$$$\mathrm{10}^{\mathrm{3}} ×\left(\mathrm{10}^{\mathrm{3}} \right)^{\mathrm{2}{n}−\mathrm{1}} =\left(\mathrm{10}^{\mathrm{6}} \right)^{{n}} \\ $$$$\mathrm{10}^{\mathrm{3}} ×\mathrm{10}^{\mathrm{6}{n}−\mathrm{3}} =\mathrm{10}^{\mathrm{6}{n}} \\ $$$$\mathrm{10}^{\mathrm{3}+\mathrm{6}{n}−\mathrm{3}} =\mathrm{10}^{\mathrm{6}{n}} \\ $$$$\mathrm{10}^{\mathrm{6}{n}} =\mathrm{10}^{\mathrm{6}{n}} \\ $$$${a}_{{n}} =\mathrm{2}{n}−\mathrm{1} \\ $$$$\left\{\left(\mathrm{1},\mathrm{1}\right),\left(\mathrm{2},\mathrm{3}\right),\left(\mathrm{3},\mathrm{5}\right),\left(\mathrm{4},\mathrm{7}\right),\left(\mathrm{5},\mathrm{9}\right),…\right\} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply