Question Number 66875 by Cmr 237 last updated on 20/Aug/19

Commented by mathmax by abdo last updated on 20/Aug/19
![convergence of this serie let ϕ(t) =(1/(t^3 sin^2 t)) with t>1 we have ϕ^′ (t) = −((3t^2 sin^2 t +2t^3 sint cost)/(t^6 sin^4 t)) ∃A>0 / for t>A ϕ^′ (t)<0 ⇒ϕ is decreazing on ]A,+∞[ so Σ_(n=1) ^∞ (1/(n^3 sin^2 n)) and ∫_1 ^(+∞) (dt/(t^3 sin^2 t)) have the same nature ∫_1 ^(+∞) (dt/(t^3 sin^2 t)) the function is continue on [1,A[ so integrable on [1,A[ and at V(+∞) lim_(t→+∞) t^2 ×(1/(t^3 sin^2 t)) =lim_(t→+∞) (1/(tsin^2 t)) = ⇒the integral converges ⇒ this serie converges....](https://www.tinkutara.com/question/Q66879.png)
$${convergence}\:{of}\:{this}\:{serie}\:\:\:{let}\:\varphi\left({t}\right)\:=\frac{\mathrm{1}}{{t}^{\mathrm{3}} {sin}^{\mathrm{2}} {t}}\:\:{with}\:{t}>\mathrm{1} \\ $$$${we}\:{have}\:\varphi^{'} \left({t}\right)\:=\:−\frac{\mathrm{3}{t}^{\mathrm{2}} {sin}^{\mathrm{2}} {t}\:+\mathrm{2}{t}^{\mathrm{3}} {sint}\:{cost}}{{t}^{\mathrm{6}} {sin}^{\mathrm{4}} {t}}\:\:\:\exists{A}>\mathrm{0}\:/\:{for}\:{t}>{A} \\ $$$$\left.\varphi^{'} \left({t}\right)<\mathrm{0}\:\Rightarrow\varphi\:{is}\:{decreazing}\:{on}\:\right]{A},+\infty\left[\:\:{so}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{3}} {sin}^{\mathrm{2}} {n}}\right. \\ $$$${and}\:\:\int_{\mathrm{1}} ^{+\infty} \:\frac{{dt}}{{t}^{\mathrm{3}} {sin}^{\mathrm{2}} {t}}\:\:{have}\:{the}\:{same}\:{nature}\: \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\frac{{dt}}{{t}^{\mathrm{3}} {sin}^{\mathrm{2}} {t}}\:\:\:\:{the}\:{function}\:{is}\:{continue}\:{on}\:\left[\mathrm{1},{A}\left[\:{so}\:{integrable}\:{on}\right.\right. \\ $$$$\left[\mathrm{1},{A}\left[\:\:\:{and}\:{at}\:{V}\left(+\infty\right)\:\:{lim}_{{t}\rightarrow+\infty} \:\:\:{t}^{\mathrm{2}} \:×\frac{\mathrm{1}}{{t}^{\mathrm{3}} {sin}^{\mathrm{2}} {t}}\:={lim}_{{t}\rightarrow+\infty} \:\:\frac{\mathrm{1}}{{tsin}^{\mathrm{2}} {t}}\:=\right.\right. \\ $$$$\Rightarrow{the}\:{integral}\:{converges}\:\Rightarrow\:{this}\:{serie}\:{converges}…. \\ $$
Commented by Prithwish sen last updated on 20/Aug/19
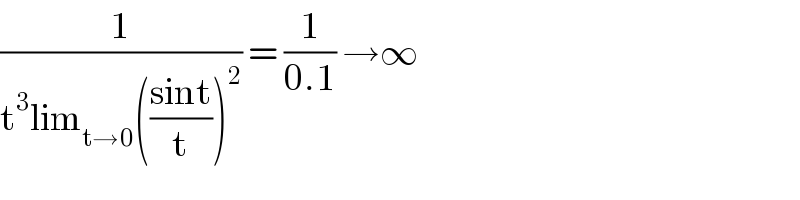
$$\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} \mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}} \left(\frac{\mathrm{sint}}{\mathrm{t}}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{0}.\mathrm{1}}\:\rightarrow\infty \\ $$
Commented by mathmax by abdo last updated on 20/Aug/19
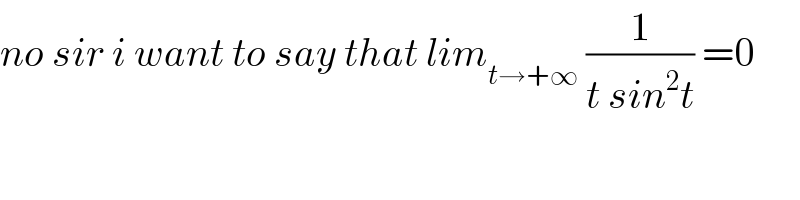
$${no}\:{sir}\:{i}\:{want}\:{to}\:{say}\:{that}\:{lim}_{{t}\rightarrow+\infty} \:\frac{\mathrm{1}}{{t}\:{sin}^{\mathrm{2}} {t}}\:=\mathrm{0} \\ $$
Commented by Prithwish sen last updated on 21/Aug/19

$$\mathrm{oh} \\ $$
