Question Number 67396 by Cmr 237 last updated on 26/Aug/19

Commented by mathmax by abdo last updated on 26/Aug/19
![let P(z) = z^(2n) +1 let determine the roots of P(z) P(z)=0 ⇔ z^(2n) =−1 ⇔ z^(2n) =e^(i(2k+1)π) if z =r e^(iθ) ⇒ 2nθ =(2k+1)π ⇒θ_k =(((2k+1)π)/(2n)) ⇒ the roots are z_k =e^((i(2k+1)π)/(2n)) with k∈[[0,2n−1]] and P(z) =Π_(k=0) ^(2n−1) (z−e^((i(2k+1)π)/(2n)) ) z_0 =e^((iπ)/(2n)) ,z_1 =e^((i3π)/(2n)) , z_2 = e^((i5π)/(2n)) .....z_(n−1) =e^((i(2n−1)π)/(2n)) z_n = e^((i(2n+1)π)/(2n)) , z_(n+1) =e^((i(2n+3)π)/(2n)) .....z_(2n−1) =e^((i(4n−1)π)/(2n)) z_0 ^− =e^((2π−(π/(2n)))i) =e^((i(4n−1)π)/(2n)) =z_(2n−1) z_1 ^− =z_(2n−2) ... ⇒ P(x) =Π_(k=0) ^(n−1) (z−z_k )(z−z_k ^− ) =Π_(k=0) ^(n−1) (z^2 −2Re(z_k )z +1) =Π_(k=0) ^(n−1) (z^2 −2cos(((2k+1)π)/(2n))z +1) z=−1 ⇒P(−1)=2 =Π_(k=0) ^(n−1) (2 +2 cos((((2k+1)π)/(2n)))) =2^n Π_(k=0) ^(n−1) (2 cos^2 ((((2k+1)π)/(4n)))) =2^(2n) { Π_(k=0) ^(n−1) cos((((2k+1)π)/(4n)))}^2 ⇒ {Π_(k=0) ^(n−1) cos((((2k+1)π)/(4n)))}^2 =(2/2^(2n) ) for k∈[[0,n−1]] cos((((2k+1)π)/(4n)))>0 ⇒ Π_(k=0) ^(n−1) cos((((2k+1)π)/(4n))) =((√2)/2^n ) changement of indice j=k+1 give Π_(j=0) ^n cos((((2j−1)π)/(4n))) =((√2)/2^n ) the equality is proved.](https://www.tinkutara.com/question/Q67404.png)
$${let}\:{P}\left({z}\right)\:=\:{z}^{\mathrm{2}{n}} \:+\mathrm{1}\:{let}\:{determine}\:{the}\:{roots}\:{of}\:{P}\left({z}\right) \\ $$$${P}\left({z}\right)=\mathrm{0}\:\Leftrightarrow\:{z}^{\mathrm{2}{n}} \:=−\mathrm{1}\:\:\Leftrightarrow\:\:{z}^{\mathrm{2}{n}} ={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi} \:\:{if}\:{z}\:={r}\:{e}^{{i}\theta} \:\:\Rightarrow \\ $$$$\mathrm{2}{n}\theta\:=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\:\Rightarrow\theta_{{k}} =\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{2}{n}}\:\Rightarrow\:{the}\:{roots}\:{are}\: \\ $$$${z}_{{k}} ={e}^{\frac{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{2}{n}}} \:\:\:{with}\:{k}\in\left[\left[\mathrm{0},\mathrm{2}{n}−\mathrm{1}\right]\right]\:\:\:{and} \\ $$$${P}\left({z}\right)\:=\prod_{{k}=\mathrm{0}} ^{\mathrm{2}{n}−\mathrm{1}} \:\:\left({z}−{e}^{\frac{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{2}{n}}} \right)\: \\ $$$${z}_{\mathrm{0}} ={e}^{\frac{{i}\pi}{\mathrm{2}{n}}} \:\:\:\:\:\:,{z}_{\mathrm{1}} ={e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{2}{n}}} \:\:,\:\:{z}_{\mathrm{2}} =\:{e}^{\frac{{i}\mathrm{5}\pi}{\mathrm{2}{n}}} \:…..{z}_{{n}−\mathrm{1}} \:={e}^{\frac{{i}\left(\mathrm{2}{n}−\mathrm{1}\right)\pi}{\mathrm{2}{n}}} \\ $$$${z}_{{n}} =\:{e}^{\frac{{i}\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}{\mathrm{2}{n}}} \:\:\:,\:{z}_{{n}+\mathrm{1}} ={e}^{\frac{{i}\left(\mathrm{2}{n}+\mathrm{3}\right)\pi}{\mathrm{2}{n}}} \:\:\:\:…..{z}_{\mathrm{2}{n}−\mathrm{1}} ={e}^{\frac{{i}\left(\mathrm{4}{n}−\mathrm{1}\right)\pi}{\mathrm{2}{n}}} \\ $$$$\overset{−} {{z}}_{\mathrm{0}} \:={e}^{\left(\mathrm{2}\pi−\frac{\pi}{\mathrm{2}{n}}\right){i}} \:={e}^{\frac{{i}\left(\mathrm{4}{n}−\mathrm{1}\right)\pi}{\mathrm{2}{n}}} \:={z}_{\mathrm{2}{n}−\mathrm{1}} \:\:\:\:\:\:\overset{−} {{z}}_{\mathrm{1}} \:\:={z}_{\mathrm{2}{n}−\mathrm{2}} \:\:\:…\:\Rightarrow \\ $$$${P}\left({x}\right)\:=\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({z}−{z}_{{k}} \right)\left({z}−\overset{−} {{z}}_{{k}} \right)\:=\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({z}^{\mathrm{2}} −\mathrm{2}{Re}\left({z}_{{k}} \right){z}\:+\mathrm{1}\right) \\ $$$$=\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({z}^{\mathrm{2}} −\mathrm{2}{cos}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{2}{n}}{z}\:+\mathrm{1}\right) \\ $$$${z}=−\mathrm{1}\:\Rightarrow{P}\left(−\mathrm{1}\right)=\mathrm{2}\:=\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left(\mathrm{2}\:+\mathrm{2}\:{cos}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{2}{n}}\right)\right) \\ $$$$=\mathrm{2}^{{n}} \:\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\left(\mathrm{2}\:{cos}^{\mathrm{2}} \left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{4}{n}}\right)\right)\:=\mathrm{2}^{\mathrm{2}{n}} \left\{\:\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:{cos}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{4}{n}}\right)\right\}^{\mathrm{2}} \:\Rightarrow \\ $$$$\left\{\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{cos}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{4}{n}}\right)\right\}^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}{n}} }\:\:\:\:{for}\:{k}\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right]\:\:{cos}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{4}{n}}\right)>\mathrm{0}\:\Rightarrow \\ $$$$\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{cos}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{4}{n}}\right)\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}^{{n}} }\:\:{changement}\:{of}\:{indice}\:{j}={k}+\mathrm{1}\:{give} \\ $$$$\prod_{{j}=\mathrm{0}} ^{{n}} \:{cos}\left(\frac{\left(\mathrm{2}{j}−\mathrm{1}\right)\pi}{\mathrm{4}{n}}\right)\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}^{{n}} }\:\:\:\:\:{the}\:{equality}\:{is}\:{proved}. \\ $$
Commented by mathmax by abdo last updated on 26/Aug/19
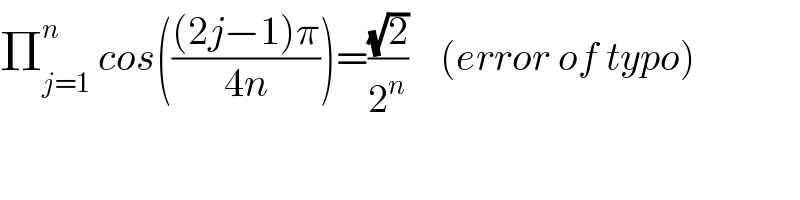
$$\prod_{{j}=\mathrm{1}} ^{{n}} \:{cos}\left(\frac{\left(\mathrm{2}{j}−\mathrm{1}\right)\pi}{\mathrm{4}{n}}\right)=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}^{{n}} }\:\:\:\:\left({error}\:{of}\:{typo}\right) \\ $$
