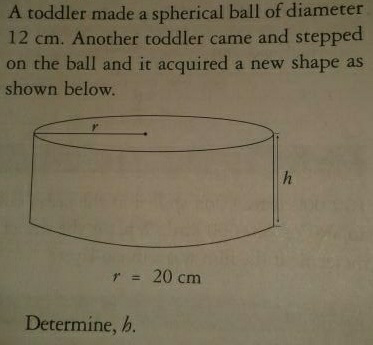
Question Number 6893 by Tawakalitu. last updated on 01/Aug/16
Commented by Rasheed Soomro last updated on 02/Aug/16
![•Surface area of sphere=4πr^2 Radius of the sphere =((12)/2)=6 cm Surface area of sphere=4π(6)^2 =144π..........(i) •Surface of the cylinder=2πr^2 +2πrh =2π(20)^2 +2π(20)h [ r=20 (given) ] =( 800+40h)π.....................(ii) •According to the question (i)=(ii) ( 800+40h)π=144π 800+40h=144 h=((144−800)/(40))=negative From 144π we can′t make cylinder of radius 20 cm.](https://www.tinkutara.com/question/Q6898.png)
$$\bullet{Surface}\:{area}\:{of}\:{sphere}=\mathrm{4}\pi{r}^{\mathrm{2}} \\ $$$$\:{Radius}\:{of}\:{the}\:\:{sphere}\:=\frac{\mathrm{12}}{\mathrm{2}}=\mathrm{6}\:{cm} \\ $$$${Surface}\:{area}\:{of}\:{sphere}=\mathrm{4}\pi\left(\mathrm{6}\right)^{\mathrm{2}} =\mathrm{144}\pi……….\left({i}\right) \\ $$$$ \\ $$$$\bullet{Surface}\:{of}\:{the}\:{cylinder}=\mathrm{2}\pi{r}^{\mathrm{2}} +\mathrm{2}\pi{rh} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\pi\left(\mathrm{20}\right)^{\mathrm{2}} +\mathrm{2}\pi\left(\mathrm{20}\right){h}\:\:\:\:\:\left[\:\:\:{r}=\mathrm{20}\:\:\left({given}\right)\:\:\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\:\mathrm{800}+\mathrm{40}{h}\right)\pi…………………\left({ii}\right) \\ $$$$\bullet{According}\:{to}\:{the}\:{question}\:\:\:\left({i}\right)=\left({ii}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\:\mathrm{800}+\mathrm{40}{h}\right)\pi=\mathrm{144}\pi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{800}+\mathrm{40}{h}=\mathrm{144} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{h}=\frac{\mathrm{144}−\mathrm{800}}{\mathrm{40}}={negative} \\ $$$$\:\:\:\:\:\:{From}\:\mathrm{144}\pi\:{we}\:{can}'{t}\:\:{make}\:\:{cylinder}\:{of}\:{radius}\:\mathrm{20}\:{cm}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by Tawakalitu. last updated on 02/Aug/16

$${Wow}\:{thanks} \\ $$
Answered by sandy_suhendra last updated on 02/Aug/16
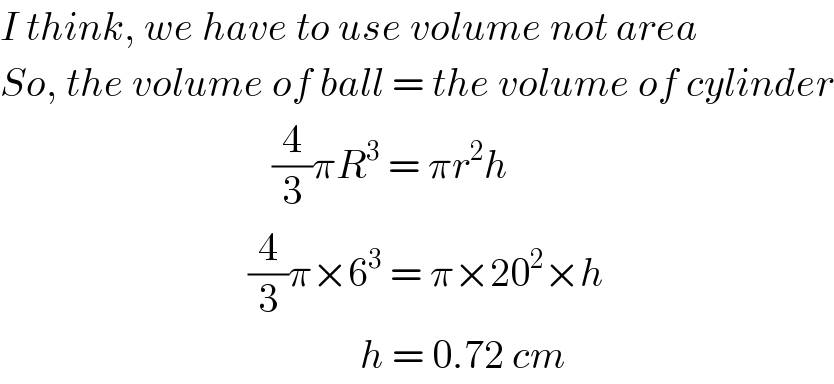
$${I}\:{think},\:{we}\:{have}\:{to}\:{use}\:{volume}\:{not}\:{area} \\ $$$${So},\:{the}\:{volume}\:{of}\:{ball}\:=\:{the}\:{volume}\:{of}\:{cylinder} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{4}}{\mathrm{3}}\pi{R}^{\mathrm{3}} \:=\:\pi{r}^{\mathrm{2}} {h} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{4}}{\mathrm{3}}\pi×\mathrm{6}^{\mathrm{3}} \:=\:\pi×\mathrm{20}^{\mathrm{2}} ×{h} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{h}\:=\:\mathrm{0}.\mathrm{72}\:{cm} \\ $$
