Question Number 70035 by TawaTawa last updated on 30/Sep/19

Commented by TawaTawa last updated on 30/Sep/19
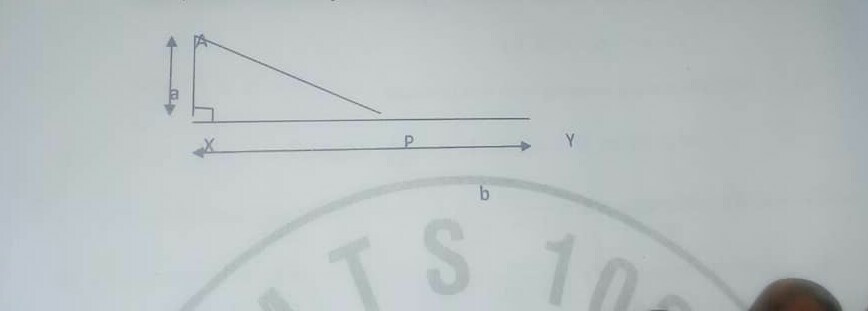
Commented by mr W last updated on 30/Sep/19
![let x=XP AP=(√(a^2 +x^2 )) PY=b−x t=((AP)/v)+((PY)/u) uvt=u(√(a^2 +x^2 ))+v(b−x) ((d(uvt))/dx)=((ux)/( (√(a^2 +x^2 ))))−v=0 ⇒ux=v(√(a^2 +x^2 )) u^2 x^2 =v^2 (a^2 +x^2 ) x^2 =((v^2 a^2 )/(u^2 −v^2 )) x=(a/( (√((u^2 /v^2 )−1)))) t_(min) =((√(a^2 +x^2 ))/v)+((b−x)/u)=(1/u)[((u^2 /v^2 )−1)x+b] ⇒t_(min) =(1/u)[a(√((u^2 /v^2 )−1))+b]](https://www.tinkutara.com/question/Q70076.png)
$${let}\:{x}={XP} \\ $$$${AP}=\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$${PY}={b}−{x} \\ $$$${t}=\frac{{AP}}{{v}}+\frac{{PY}}{{u}} \\ $$$${uvt}={u}\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }+{v}\left({b}−{x}\right) \\ $$$$\frac{{d}\left({uvt}\right)}{{dx}}=\frac{{ux}}{\:\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }}−{v}=\mathrm{0} \\ $$$$\Rightarrow{ux}={v}\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$${u}^{\mathrm{2}} {x}^{\mathrm{2}} ={v}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{x}^{\mathrm{2}} \right) \\ $$$${x}^{\mathrm{2}} =\frac{{v}^{\mathrm{2}} {a}^{\mathrm{2}} }{{u}^{\mathrm{2}} −{v}^{\mathrm{2}} } \\ $$$${x}=\frac{{a}}{\:\sqrt{\frac{{u}^{\mathrm{2}} }{{v}^{\mathrm{2}} }−\mathrm{1}}} \\ $$$${t}_{{min}} =\frac{\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }}{{v}}+\frac{{b}−{x}}{{u}}=\frac{\mathrm{1}}{{u}}\left[\left(\frac{{u}^{\mathrm{2}} }{{v}^{\mathrm{2}} }−\mathrm{1}\right){x}+{b}\right] \\ $$$$\Rightarrow{t}_{{min}} =\frac{\mathrm{1}}{{u}}\left[{a}\sqrt{\frac{{u}^{\mathrm{2}} }{{v}^{\mathrm{2}} }−\mathrm{1}}+{b}\right] \\ $$
Commented by TawaTawa last updated on 30/Sep/19
$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Commented by TawaTawa last updated on 30/Sep/19
$$\mathrm{Sir},\:\mathrm{help}\:\mathrm{me}\:\mathrm{check}\:\mathrm{question}\:\:\mathrm{70048} \\ $$
