Question Number 70446 by oyemi kemewari last updated on 04/Oct/19
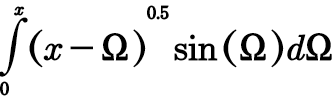
Commented by oyemi kemewari last updated on 04/Oct/19
please help me solve this question
Commented by mathmax by abdo last updated on 04/Oct/19
![its only a try let f(x)=∫_0 ^x (√(x−t))sint dt changement (√(x−t))=u give x−t=u^2 ⇒t=x−u^2 ⇒f(x)=−∫_0 ^(√x) usin(x−u^2 )(−2u)du =2 ∫_0 ^(√x) u^2 sin(x−u^2 )du =∫_0 ^(√x) u(2usin(x−u^2 ))du by parts f=u and g^′ =2usin(x−u^2 ) ⇒ f(x)=[u cos(x−u^2 )]_0 ^(√x) −∫_0 ^(√x) cos(x−u^2 )du =(√x)cos((√x)−x) −∫_0 ^(√x) (cosx cos(u^2 )+sinx sin(u^2 )du =(√x)cos((√x)−x)−cosx ∫_0 ^(√x) cos(u^2 )du −sinx∫_0 ^(√x) sin(u^2 )du](https://www.tinkutara.com/question/Q70466.png)
$${its}\:{only}\:{a}\:{try}\:{let}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \sqrt{{x}−{t}}{sint}\:{dt}\:\:{changement}\:\sqrt{{x}−{t}}={u}\:{give} \\ $$$${x}−{t}={u}^{\mathrm{2}} \:\Rightarrow{t}={x}−{u}^{\mathrm{2}} \:\Rightarrow{f}\left({x}\right)=−\int_{\mathrm{0}} ^{\sqrt{{x}}} {usin}\left({x}−{u}^{\mathrm{2}} \right)\left(−\mathrm{2}{u}\right){du} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{{x}}} {u}^{\mathrm{2}} {sin}\left({x}−{u}^{\mathrm{2}} \right){du}\:\:=\int_{\mathrm{0}} ^{\sqrt{{x}}} {u}\left(\mathrm{2}{usin}\left({x}−{u}^{\mathrm{2}} \right)\right){du} \\ $$$${by}\:{parts}\:\:{f}={u}\:{and}\:{g}^{'} =\mathrm{2}{usin}\left({x}−{u}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${f}\left({x}\right)=\left[{u}\:{cos}\left({x}−{u}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\sqrt{{x}}} \:\:\:−\int_{\mathrm{0}} ^{\sqrt{{x}}} {cos}\left({x}−{u}^{\mathrm{2}} \right){du} \\ $$$$=\sqrt{{x}}{cos}\left(\sqrt{{x}}−{x}\right)\:−\int_{\mathrm{0}} ^{\sqrt{{x}}} \left({cosx}\:{cos}\left({u}^{\mathrm{2}} \right)+{sinx}\:{sin}\left({u}^{\mathrm{2}} \right){du}\right. \\ $$$$=\sqrt{{x}}{cos}\left(\sqrt{{x}}−{x}\right)−{cosx}\:\int_{\mathrm{0}} ^{\sqrt{{x}}} \:{cos}\left({u}^{\mathrm{2}} \right){du}\:−{sinx}\int_{\mathrm{0}} ^{\sqrt{{x}}} \:{sin}\left({u}^{\mathrm{2}} \right){du} \\ $$
Commented by MJS last updated on 04/Oct/19
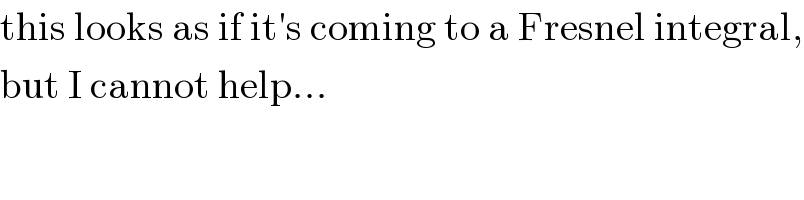
$$\mathrm{this}\:\mathrm{looks}\:\mathrm{as}\:\mathrm{if}\:\mathrm{it}'\mathrm{s}\:\mathrm{coming}\:\mathrm{to}\:\mathrm{a}\:\mathrm{Fresnel}\:\mathrm{integral}, \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{cannot}\:\mathrm{help}… \\ $$
Commented by mathmax by abdo last updated on 04/Oct/19

$${you}\:{are}\:{right}\:{sir}. \\ $$
