Question Number 72408 by ajfour last updated on 28/Oct/19

Commented by ajfour last updated on 28/Oct/19

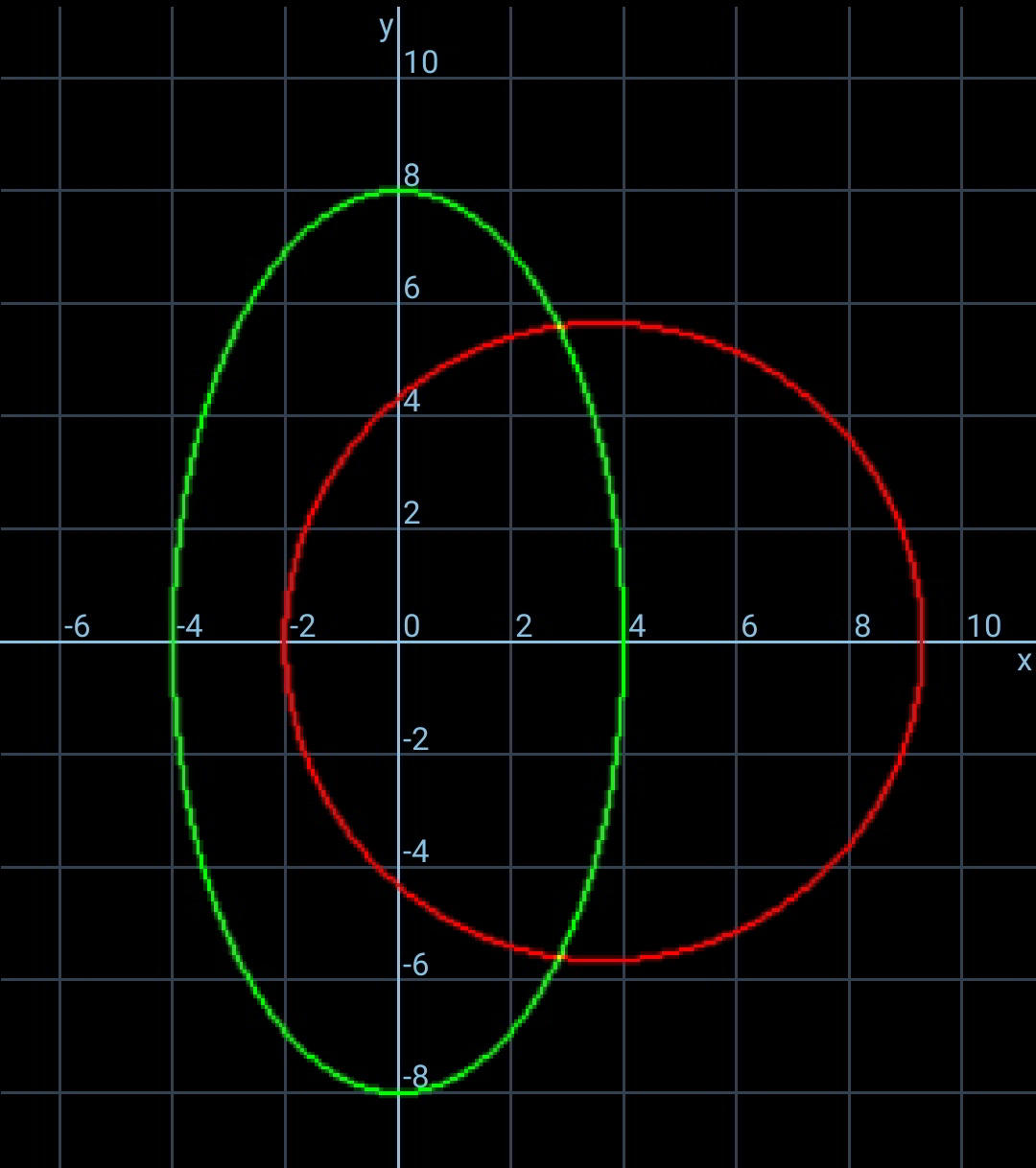
$${All}\:{three}\:{coloured}\:{regions}\:{A},\:{B},\:{C} \\ $$$${have}\:{the}\:{same}\:{area}.\:{Center}\:{of} \\ $$$${circle}\:{lies}\:{on}\:{major}\:{axis}\:{of}\:{ellipse}. \\ $$$${Locate}\:{the}\:{center}\:{of}\:{circle}\:{in}\:{terms}\: \\ $$$${of}\:{ellipse}\:{parameters}\:{a}\:{and}\:{b}. \\ $$
Answered by mr W last updated on 28/Oct/19

Commented by mr W last updated on 29/Oct/19
![eqn. of circle: (x−h)^2 +y^2 =r^2 eqn. of ellipse: (x^2 /a^2 )+(y^2 /b^2 )=1 (x^2 /a^2 )+((r^2 −(x−h)^2 )/b^2 )=1 b^2 x^2 +a^2 r^2 −a^2 (x^2 −2hx+h^2 )=a^2 b^2 (a^2 −b^2 )x^2 −2a^2 hx+a^2 (b^2 +h^2 −r^2 )=0 x=((a^2 h−a(√(a^2 h^2 −(a^2 −b^2 )(b^2 +h^2 −r^2 ))))/(a^2 −b^2 )) x=((a^2 h−a(√((a^2 −b^2 )(r^2 −b^2 )+h^2 b^2 )))/(a^2 −b^2 ))=k area of circle=area of ellipse πr^2 =πab ⇒r^2 =ab with λ=(b/a), η=(h/a) (k/a)=κ=((η−(√(λ(1−λ)(1−λ^2 )+λ^2 η^2 )))/(1−λ^2 )) 2∫_(h−r) ^k (√(r^2 −(x−h)^2 ))dx+2∫_k ^a b(√(1−(x^2 /a^2 )))dx=((πab)/2) ∫_(h−(√λ)a) ^k (√(λ−((x/a)−(h/a))^2 ))d((x/a))+λ∫_k ^a (√(1−(x^2 /a^2 )))d((x/a))=((πλ)/4) ∫_(η−(√λ)) ^κ (√(λ−(ξ−η)^2 ))dξ+λ∫_κ ^1 (√(1−ξ^2 ))dξ=((πλ)/4) (1/2)[λ sin^(−1) ((ξ−η)/( (√λ)))+(ξ−η)(√(λ−(ξ−η)^2 ))]_(η−(√λ)) ^κ +(λ/2)[sin^(−1) ξ+ξ(√(1−ξ^2 ))]_κ ^1 =((πλ)/4) ⇒ sin^(−1) ((κ−η)/( (√λ)))+((κ−η)/( (√λ)))(√(1−(((κ−η)/( (√λ))))^2 ))+(π/2)=sin^(−1) κ+κ(√(1−κ^2 )) this is an eqn. for η in terms of λ. examples: λ=0.5 ⇒ η=0.6432 λ=0.75 ⇒ η=0.7441 λ=2 ⇒ η=0.9096](https://www.tinkutara.com/question/Q72423.png)
$${eqn}.\:{of}\:{circle}: \\ $$$$\left({x}−{h}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${eqn}.\:{of}\:{ellipse}: \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} −\left({x}−{h}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} {r}^{\mathrm{2}} −{a}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{2}{hx}+{h}^{\mathrm{2}} \right)={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){x}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} {hx}+{a}^{\mathrm{2}} \left({b}^{\mathrm{2}} +{h}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${x}=\frac{{a}^{\mathrm{2}} {h}−{a}\sqrt{{a}^{\mathrm{2}} {h}^{\mathrm{2}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} +{h}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)}}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$${x}=\frac{{a}^{\mathrm{2}} {h}−{a}\sqrt{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({r}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)+{h}^{\mathrm{2}} {b}^{\mathrm{2}} }}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }={k} \\ $$$${area}\:{of}\:{circle}={area}\:{of}\:{ellipse} \\ $$$$\pi{r}^{\mathrm{2}} =\pi{ab} \\ $$$$\Rightarrow{r}^{\mathrm{2}} ={ab} \\ $$$${with}\:\lambda=\frac{{b}}{{a}},\:\eta=\frac{{h}}{{a}} \\ $$$$\frac{{k}}{{a}}=\kappa=\frac{\eta−\sqrt{\lambda\left(\mathrm{1}−\lambda\right)\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)+\lambda^{\mathrm{2}} \eta^{\mathrm{2}} }}{\mathrm{1}−\lambda^{\mathrm{2}} } \\ $$$$\mathrm{2}\int_{{h}−{r}} ^{{k}} \sqrt{{r}^{\mathrm{2}} −\left({x}−{h}\right)^{\mathrm{2}} }{dx}+\mathrm{2}\int_{{k}} ^{{a}} {b}\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}{dx}=\frac{\pi{ab}}{\mathrm{2}} \\ $$$$\int_{{h}−\sqrt{\lambda}{a}} ^{{k}} \sqrt{\lambda−\left(\frac{{x}}{{a}}−\frac{{h}}{{a}}\right)^{\mathrm{2}} }{d}\left(\frac{{x}}{{a}}\right)+\lambda\int_{{k}} ^{{a}} \sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}{d}\left(\frac{{x}}{{a}}\right)=\frac{\pi\lambda}{\mathrm{4}} \\ $$$$\int_{\eta−\sqrt{\lambda}} ^{\kappa} \sqrt{\lambda−\left(\xi−\eta\right)^{\mathrm{2}} }{d}\xi+\lambda\int_{\kappa} ^{\mathrm{1}} \sqrt{\mathrm{1}−\xi^{\mathrm{2}} }{d}\xi=\frac{\pi\lambda}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\lambda\:\mathrm{sin}^{−\mathrm{1}} \frac{\xi−\eta}{\:\sqrt{\lambda}}+\left(\xi−\eta\right)\sqrt{\lambda−\left(\xi−\eta\right)^{\mathrm{2}} }\right]_{\eta−\sqrt{\lambda}} ^{\kappa} +\frac{\lambda}{\mathrm{2}}\left[\mathrm{sin}^{−\mathrm{1}} \xi+\xi\sqrt{\mathrm{1}−\xi^{\mathrm{2}} }\right]_{\kappa} ^{\mathrm{1}} =\frac{\pi\lambda}{\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{sin}^{−\mathrm{1}} \frac{\kappa−\eta}{\:\sqrt{\lambda}}+\frac{\kappa−\eta}{\:\sqrt{\lambda}}\sqrt{\mathrm{1}−\left(\frac{\kappa−\eta}{\:\sqrt{\lambda}}\right)^{\mathrm{2}} }+\frac{\pi}{\mathrm{2}}=\mathrm{sin}^{−\mathrm{1}} \kappa+\kappa\sqrt{\mathrm{1}−\kappa^{\mathrm{2}} } \\ $$$${this}\:{is}\:{an}\:{eqn}.\:{for}\:\eta\:{in}\:{terms}\:{of}\:\lambda. \\ $$$$ \\ $$$${examples}: \\ $$$$\lambda=\mathrm{0}.\mathrm{5}\:\Rightarrow\:\eta=\mathrm{0}.\mathrm{6432} \\ $$$$\lambda=\mathrm{0}.\mathrm{75}\:\Rightarrow\:\eta=\mathrm{0}.\mathrm{7441} \\ $$$$\lambda=\mathrm{2}\:\Rightarrow\:\eta=\mathrm{0}.\mathrm{9096} \\ $$
Commented by ajfour last updated on 28/Oct/19

$${Thanks}\:{sir}… \\ $$$${I}\:{think},\:{all}\:{thats}\:{possible},\:{you} \\ $$$${did}\:{it}! \\ $$
Commented by mr W last updated on 28/Oct/19

Commented by mr W last updated on 29/Oct/19
Commented by ajfour last updated on 29/Oct/19

$$\mathcal{E}{xcellent}\:{sir}!\:{how}\:{about}\:{the}\:\mathrm{3}{D} \\ $$$${analogue}\:{when}\:{the}\:{three}\: \\ $$$${compartment}\:{volumes}\:{be}\:{equal}? \\ $$$${i}\:{just}\:{wonder}.. \\ $$
Commented by ajfour last updated on 29/Oct/19

$${x}={h}−{r}\mathrm{cos}\:\theta\:,\:{y}={r}\mathrm{sin}\:\theta\:,\:\:{r}=\sqrt{{ab}} \\ $$$$\frac{\left({h}−{r}\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${let}\:\mathrm{cos}\:\theta={t} \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} \left({h}^{\mathrm{2}} −\mathrm{2}{hrt}+{r}^{\mathrm{2}} {t}^{\mathrm{2}} \right)+{a}^{\mathrm{2}} {r}^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\:\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){r}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} {hrt}−\left({b}^{\mathrm{2}} {h}^{\mathrm{2}} +{a}^{\mathrm{2}} {r}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${t}=\frac{−{b}^{\mathrm{2}} {hr}+\sqrt{{b}^{\mathrm{4}} {h}^{\mathrm{2}} {r}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} {h}^{\mathrm{2}} +{a}^{\mathrm{2}} {r}^{\mathrm{2}} \right)}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){r}^{\mathrm{2}} } \\ $$$${ellipse} \\ $$$${y}=\frac{{b}}{{a}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$${A}=\frac{{b}}{{a}}\int_{−{a}} ^{\:{h}−{rt}} \sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}−\frac{{r}^{\mathrm{2}} \theta}{\mathrm{2}}+\frac{{r}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{2}} \\ $$$$\:\:\:\:=\:\frac{\pi{ab}}{\mathrm{4}} \\ $$$$\left\{\frac{{x}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{{x}}{{a}}\right\}_{−{a}} ^{{h}−{rt}} \\ $$$$\:\:\:−\frac{{r}^{\mathrm{2}} \theta}{\mathrm{2}}+\frac{{r}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{2}}=\frac{\pi{ab}}{\mathrm{4}} \\ $$$$\Rightarrow\:\:\left(\frac{{h}−{rt}}{\mathrm{2}}\right)\sqrt{{a}^{\mathrm{2}} −\left({h}−{rt}\right)^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{{h}−{rt}}{{a}}\right)+\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\:\:\:\:\:−\frac{{r}^{\mathrm{2}} \mathrm{cos}^{−\mathrm{1}} {t}}{\mathrm{2}}+\frac{{r}^{\mathrm{2}} {t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{2}}=\frac{\pi{ab}}{\mathrm{4}} \\ $$$${t}=\mathrm{cos}\:\theta\:{is}\:{obtained}\:{from}\:{above}\:{eq}. \\ $$$${Then}\:{to}\:{find}\:{h}, \\ $$$${t}=\frac{−{b}^{\mathrm{2}} {hr}+\sqrt{{b}^{\mathrm{4}} {h}^{\mathrm{2}} {r}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} {h}^{\mathrm{2}} +{a}^{\mathrm{2}} {r}^{\mathrm{2}} \right)}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){r}^{\mathrm{2}} } \\ $$$$.. \\ $$
