Question Number 73503 by ajfour last updated on 13/Nov/19
Commented by ajfour last updated on 13/Nov/19

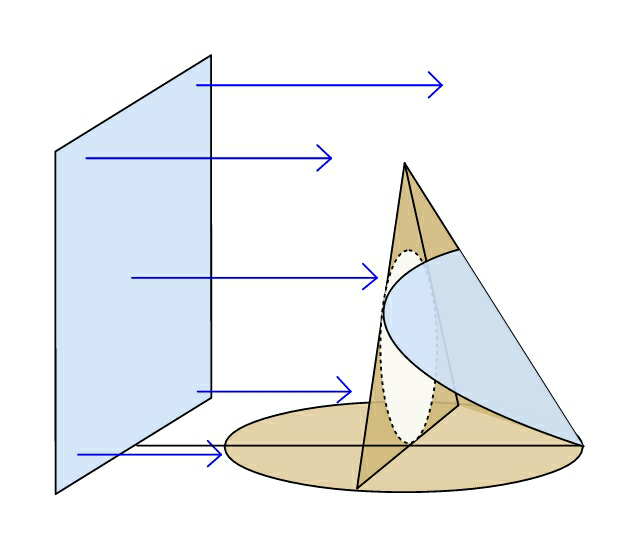
$${Find}\:{the}\:{illuminated}\:{curved} \\ $$$${area}\:{of}\:{cone}\:{with}\:{radius}\:{a},\:{and} \\ $$$${altitude}\:{a}\sqrt{\mathrm{3}}\:.\:{Only}\:{the}\:{right}\:{half} \\ $$$${of}\:{cone}\:{is}\:{there}\:{with}\:{left}\:{half} \\ $$$${covered}\:{but}\:{with}\:{a}\:{largest}\:{circular} \\ $$$${opening}\:{in}\:{it}.\:{Light}\:{is}\:{incident} \\ $$$${from}\:{a}\:{plane}\:{wall}\:{sending} \\ $$$${horizontal}\:{parallel}\:{rays}.\:\:\:\:\:\:\:\: \\ $$
Commented by mr W last updated on 14/Nov/19
$${how}\:{is}\:{the}\:{answer},\:{if}\:{the}\:{opening}\:{is} \\ $$$${a}\:{square}? \\ $$
Answered by mr W last updated on 13/Nov/19
Commented by mr W last updated on 14/Nov/19
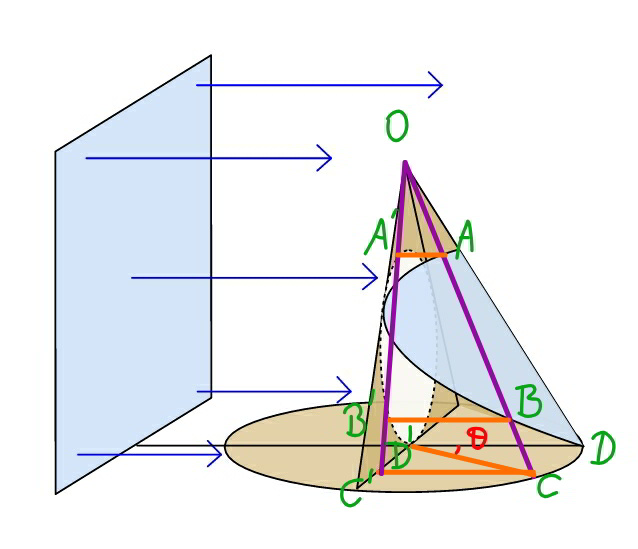
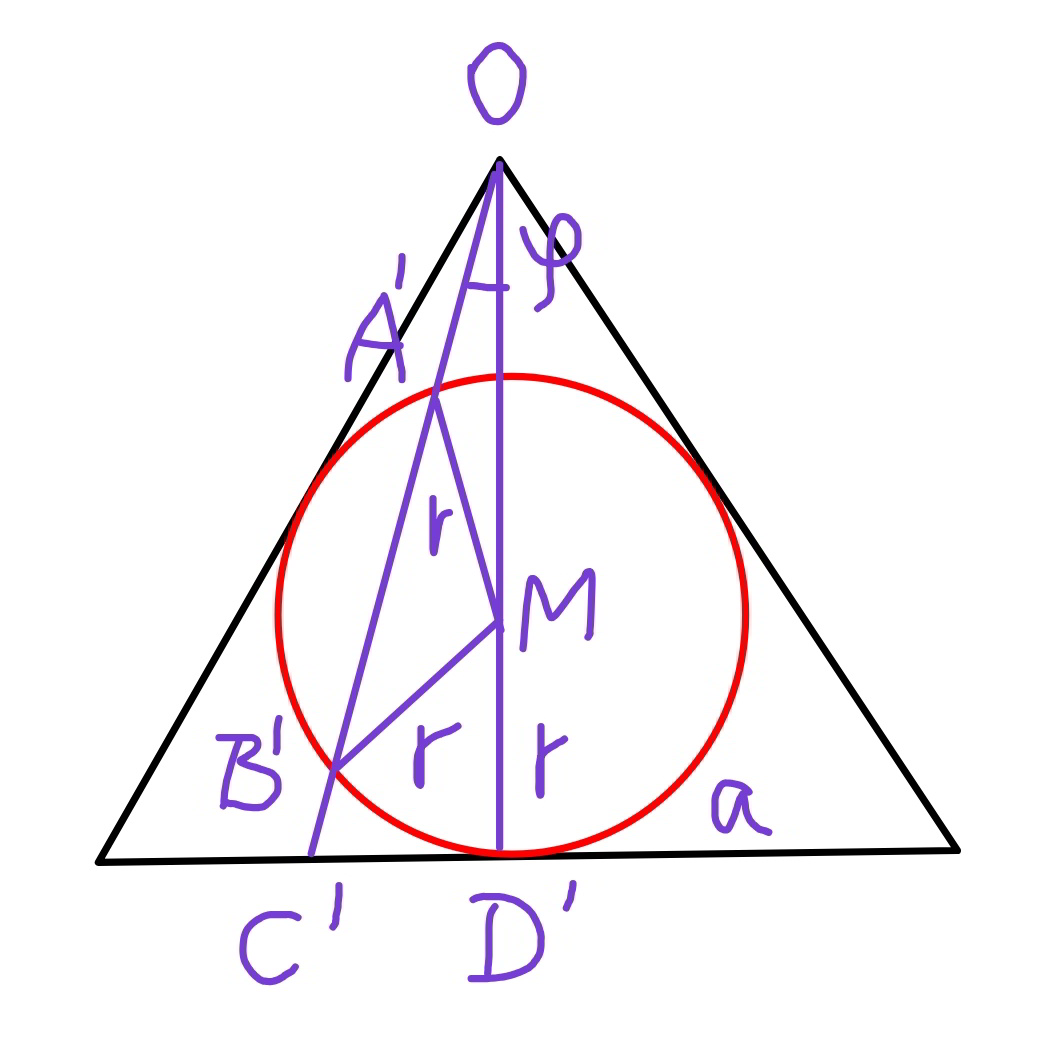
![OD′=(√3)a OC=OD=2a C′D′=a sin θ OC′=(√(3a^2 +a^2 sin^2 θ))=a(√(3+sin^2 θ)) ∠C′OD′=ϕ tan ϕ=((sin θ)/( (√3))) ⇒cos ϕ=((√3)/( (√(3+sin^2 θ)))) ⇒4cos^2 ϕ−3=((3 cos^2 θ)/(3+sin^2 θ)) r=(a/( (√3))) OM=((2a)/( (√3))) r^2 =OA′^2 +OM^2 −2×OA′×OM cos ϕ (a^2 /3)=OA′^2 +((4a^2 )/3)−2×OA′×((2a)/( (√3))) cos ϕ OA′^2 −OA′×((4a)/( (√3))) cos ϕ+a^2 =0 OA′=((2a cos ϕ)/( (√3)))−(√(((4a^2 cos^2 ϕ)/3)−a^2 )) OA′=(((2 cos ϕ−(√(4 cos^2 ϕ−3)))a)/( (√3))) OB′=(((2 cos ϕ+(√(4 cos^2 ϕ−3)))a)/( (√3))) ((OA)/(OA′))=((OC)/(OC′))=(2/( (√(3+sin^2 θ)))) ⇒OA=((2(2 cos ϕ−(√(4 cos^2 ϕ−3)))a)/( (√(3(3+sin^2 θ))))) similarly ⇒OB=((2(2 cos ϕ+(√(4 cos^2 ϕ−3)))a)/( (√(3(3+sin^2 θ))))) CD^(⌢) =a θ=2a φ ⇒φ=(θ/2) dA=(1/2)(OB^2 −OA^2 )dφ dA=2a^2 [(((2 cos ϕ+(√(4 cos^2 ϕ−3)))^2 −(2 cos ϕ−(√(4 cos^2 ϕ−3)))^2 )/(3(3+sin^2 θ)))]dφ dA=((8a^2 )/3)[((cos ϕ (√(4 cos^2 ϕ−3)))/(3+sin^2 θ))]dθ dA=((8a^2 cos θ dθ)/((3+sin^2 θ)^2 )) A=2×8a^2 ∫_0 ^(π/2) ((cos θ dθ)/((3+sin^2 θ)^2 )) A=16a^2 ∫_0 ^(π/2) ((d (sin θ))/((3+sin^2 θ)^2 )) A=16a^2 ∫_0 ^1 (dt/((3+t^2 )^2 )) A=((8a^2 )/3)[(1/( (√3))) tan^(−1) (t/( (√3)))+(t/(t^2 +3))]_0 ^1 A=((8a^2 )/3)((1/( (√3)))×(π/6)+(1/4)) ⇒A=((2(2(√3)π+9)a^2 )/(27))≈1.4728a^2 Area of surface of semi−cone: (1/2)×(π/2)×(2a)^2 =π a^2 ((1.4728a^2 )/(πa^2 ))=0.47=47% i.e. 47% of the semi cone surface is lighted.](https://www.tinkutara.com/question/Q73609.png)
$${OD}'=\sqrt{\mathrm{3}}{a} \\ $$$${OC}={OD}=\mathrm{2}{a} \\ $$$${C}'{D}'={a}\:\mathrm{sin}\:\theta \\ $$$${OC}'=\sqrt{\mathrm{3}{a}^{\mathrm{2}} +{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}={a}\sqrt{\mathrm{3}+\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$\angle{C}'{OD}'=\varphi \\ $$$$\mathrm{tan}\:\varphi=\frac{\mathrm{sin}\:\theta}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\mathrm{cos}\:\varphi=\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{3}+\mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$$\Rightarrow\mathrm{4cos}^{\mathrm{2}} \:\varphi−\mathrm{3}=\frac{\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{3}+\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$${r}=\frac{{a}}{\:\sqrt{\mathrm{3}}} \\ $$$${OM}=\frac{\mathrm{2}{a}}{\:\sqrt{\mathrm{3}}} \\ $$$${r}^{\mathrm{2}} ={OA}'^{\mathrm{2}} +{OM}^{\mathrm{2}} −\mathrm{2}×{OA}'×{OM}\:\mathrm{cos}\:\varphi \\ $$$$\frac{{a}^{\mathrm{2}} }{\mathrm{3}}={OA}'^{\mathrm{2}} +\frac{\mathrm{4}{a}^{\mathrm{2}} }{\mathrm{3}}−\mathrm{2}×{OA}'×\frac{\mathrm{2}{a}}{\:\sqrt{\mathrm{3}}}\:\mathrm{cos}\:\varphi \\ $$$${OA}'^{\mathrm{2}} −{OA}'×\frac{\mathrm{4}{a}}{\:\sqrt{\mathrm{3}}}\:\mathrm{cos}\:\varphi+{a}^{\mathrm{2}} =\mathrm{0} \\ $$$${OA}'=\frac{\mathrm{2}{a}\:\mathrm{cos}\:\varphi}{\:\sqrt{\mathrm{3}}}−\sqrt{\frac{\mathrm{4}{a}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\varphi}{\mathrm{3}}−{a}^{\mathrm{2}} } \\ $$$${OA}'=\frac{\left(\mathrm{2}\:\mathrm{cos}\:\varphi−\sqrt{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\varphi−\mathrm{3}}\right){a}}{\:\sqrt{\mathrm{3}}} \\ $$$${OB}'=\frac{\left(\mathrm{2}\:\mathrm{cos}\:\varphi+\sqrt{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\varphi−\mathrm{3}}\right){a}}{\:\sqrt{\mathrm{3}}} \\ $$$$\frac{{OA}}{{OA}'}=\frac{{OC}}{{OC}'}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}+\mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$$\Rightarrow{OA}=\frac{\mathrm{2}\left(\mathrm{2}\:\mathrm{cos}\:\varphi−\sqrt{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\varphi−\mathrm{3}}\right){a}}{\:\sqrt{\mathrm{3}\left(\mathrm{3}+\mathrm{sin}^{\mathrm{2}} \:\theta\right)}} \\ $$$${similarly} \\ $$$$\Rightarrow{OB}=\frac{\mathrm{2}\left(\mathrm{2}\:\mathrm{cos}\:\varphi+\sqrt{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\varphi−\mathrm{3}}\right){a}}{\:\sqrt{\mathrm{3}\left(\mathrm{3}+\mathrm{sin}^{\mathrm{2}} \:\theta\right)}} \\ $$$$\overset{\frown} {{CD}}={a}\:\theta=\mathrm{2}{a}\:\phi \\ $$$$\Rightarrow\phi=\frac{\theta}{\mathrm{2}} \\ $$$${dA}=\frac{\mathrm{1}}{\mathrm{2}}\left({OB}^{\mathrm{2}} −{OA}^{\mathrm{2}} \right){d}\phi \\ $$$${dA}=\mathrm{2}{a}^{\mathrm{2}} \left[\frac{\left(\mathrm{2}\:\mathrm{cos}\:\varphi+\sqrt{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\varphi−\mathrm{3}}\right)^{\mathrm{2}} −\left(\mathrm{2}\:\mathrm{cos}\:\varphi−\sqrt{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\varphi−\mathrm{3}}\right)^{\mathrm{2}} }{\mathrm{3}\left(\mathrm{3}+\mathrm{sin}^{\mathrm{2}} \:\theta\right)}\right]{d}\phi \\ $$$${dA}=\frac{\mathrm{8}{a}^{\mathrm{2}} }{\mathrm{3}}\left[\frac{\mathrm{cos}\:\varphi\:\sqrt{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\varphi−\mathrm{3}}}{\mathrm{3}+\mathrm{sin}^{\mathrm{2}} \:\theta}\right]{d}\theta \\ $$$${dA}=\frac{\mathrm{8}{a}^{\mathrm{2}} \:\mathrm{cos}\:\theta\:{d}\theta}{\left(\mathrm{3}+\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$${A}=\mathrm{2}×\mathrm{8}{a}^{\mathrm{2}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}\:\theta\:{d}\theta}{\left(\mathrm{3}+\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$${A}=\mathrm{16}{a}^{\mathrm{2}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\:\left(\mathrm{sin}\:\theta\right)}{\left(\mathrm{3}+\mathrm{sin}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} } \\ $$$${A}=\mathrm{16}{a}^{\mathrm{2}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\left(\mathrm{3}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${A}=\frac{\mathrm{8}{a}^{\mathrm{2}} }{\mathrm{3}}\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{tan}^{−\mathrm{1}} \frac{{t}}{\:\sqrt{\mathrm{3}}}+\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{3}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${A}=\frac{\mathrm{8}{a}^{\mathrm{2}} }{\mathrm{3}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}×\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\Rightarrow{A}=\frac{\mathrm{2}\left(\mathrm{2}\sqrt{\mathrm{3}}\pi+\mathrm{9}\right){a}^{\mathrm{2}} }{\mathrm{27}}\approx\mathrm{1}.\mathrm{4728}{a}^{\mathrm{2}} \\ $$$$ \\ $$$${Area}\:{of}\:{surface}\:{of}\:{semi}−{cone}: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{\mathrm{2}}×\left(\mathrm{2}{a}\right)^{\mathrm{2}} =\pi\:{a}^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}.\mathrm{4728}{a}^{\mathrm{2}} }{\pi{a}^{\mathrm{2}} }=\mathrm{0}.\mathrm{47}=\mathrm{47\%} \\ $$$${i}.{e}.\:\mathrm{47\%}\:{of}\:{the}\:{semi}\:{cone}\:{surface}\:{is} \\ $$$${lighted}. \\ $$
Commented by mr W last updated on 13/Nov/19
Commented by mr W last updated on 13/Nov/19
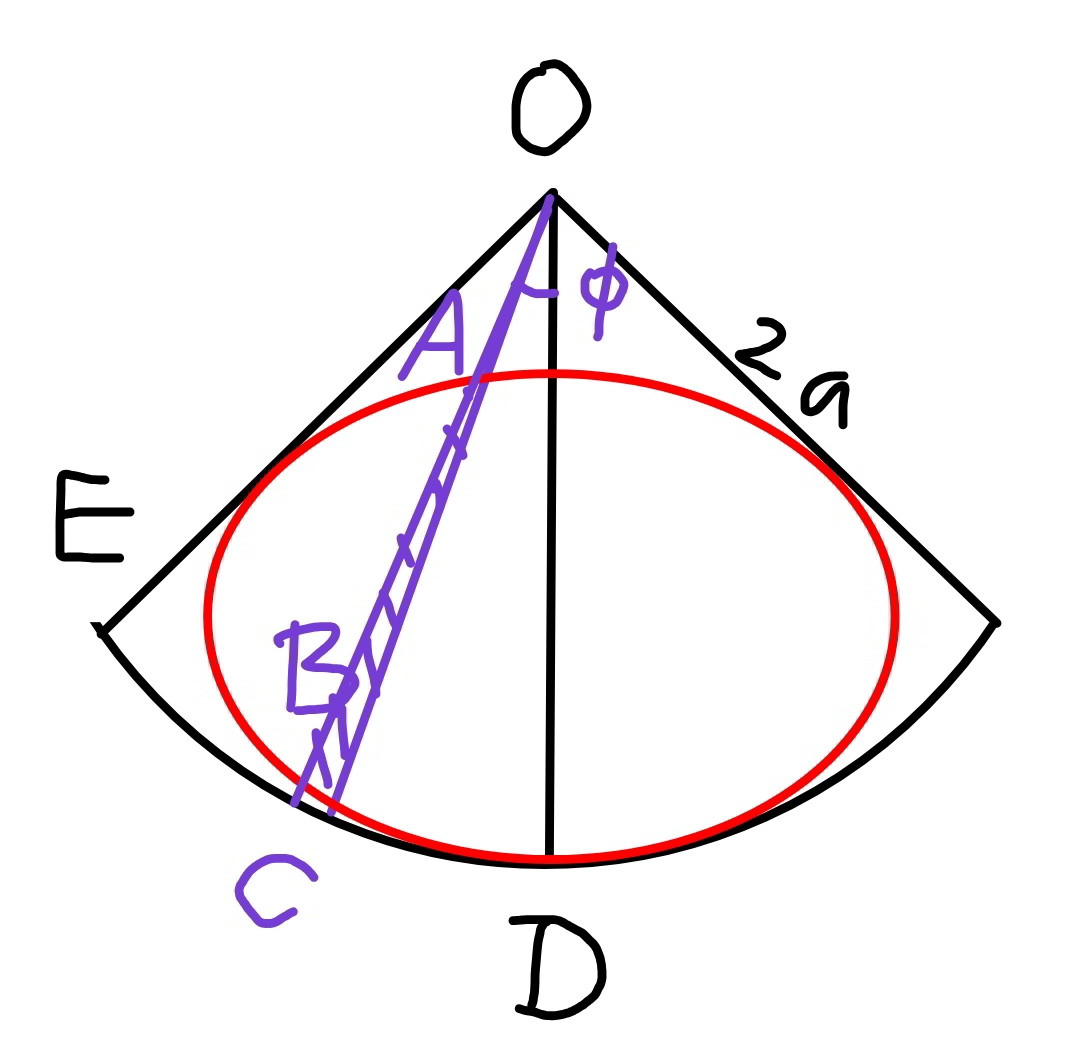
Commented by mr W last updated on 13/Nov/19

$${this}\:{is}\:{how}\:{the}\:{lighted}\:{area}\:{really} \\ $$$${looks}\:{like}: \\ $$
Commented by mr W last updated on 14/Nov/19
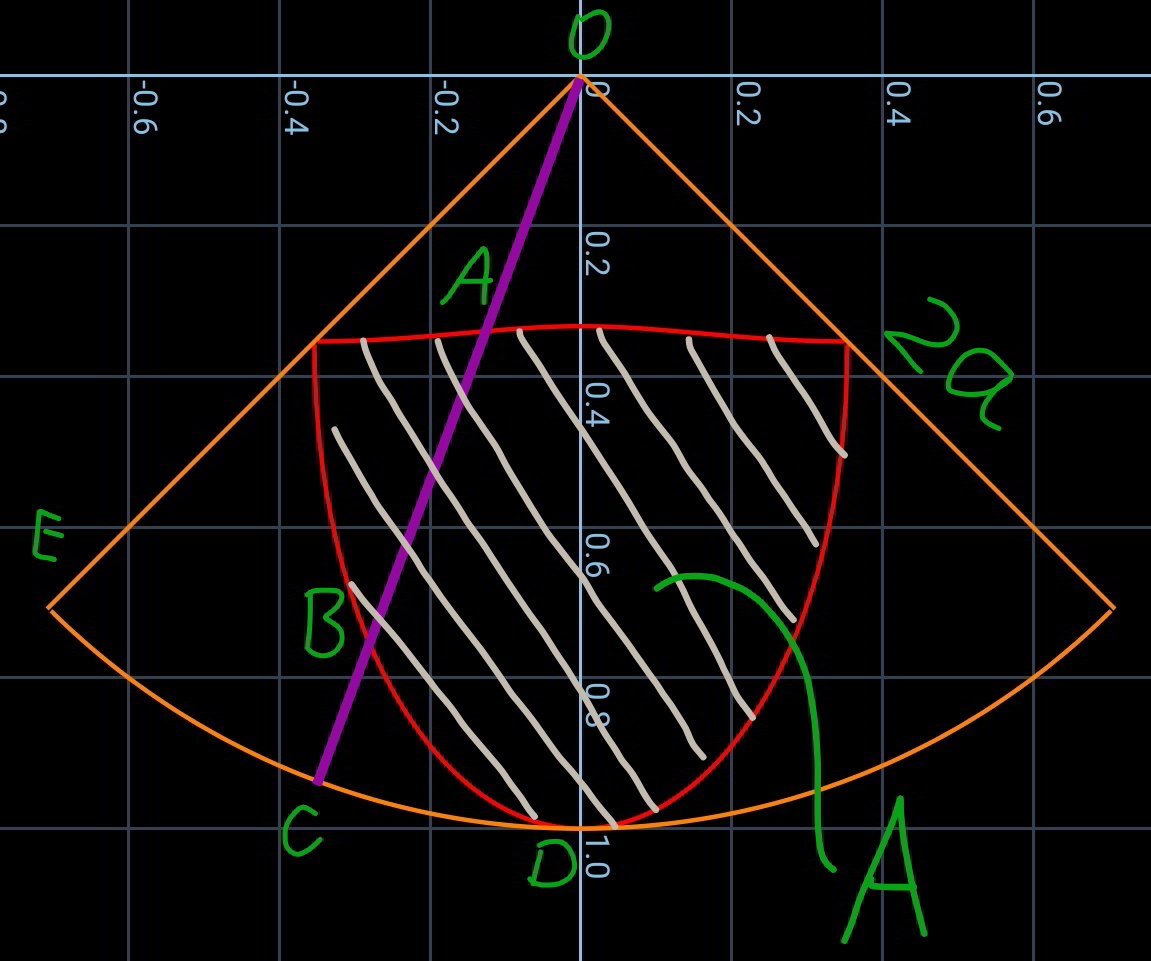
Commented by ajfour last updated on 14/Nov/19
$${Thanks}\:{Sir},\:\mathcal{SPLENDID}\:{solution}! \\ $$$$\left({nice}\:{reverse}\:{swing}\:!\right). \\ $$
Commented by mr W last updated on 14/Nov/19
$${thanks}\:{for}\:{viewing}\:{sir}!\:{it}'{s}\:{a}\:{very} \\ $$$${nice}\:{question}! \\ $$
