Question Number 8553 by Sopheak last updated on 16/Oct/16

Commented by Yozzias last updated on 16/Oct/16
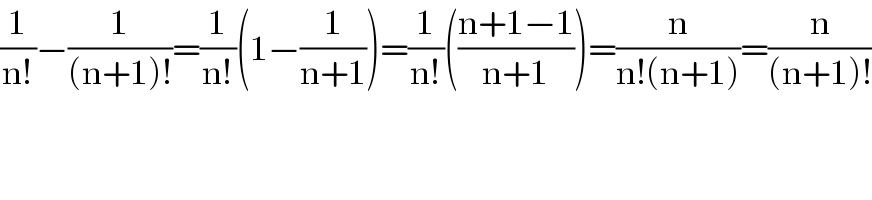
$$\frac{\mathrm{1}}{\mathrm{n}!}−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!}=\frac{\mathrm{1}}{\mathrm{n}!}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{n}!}\left(\frac{\mathrm{n}+\mathrm{1}−\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)=\frac{\mathrm{n}}{\mathrm{n}!\left(\mathrm{n}+\mathrm{1}\right)}=\frac{\mathrm{n}}{\left(\mathrm{n}+\mathrm{1}\right)!} \\ $$
Answered by Yozzias last updated on 16/Oct/16
![S=Σ_(r=1) ^n (r/((r+1)!))=Σ_(r=1) ^n [(1/(r!))−(1/((r+1)!))]=Σ_(r=1) ^n {f(r)−f(r+1)} S={f(1)−f(2)}+{f(2)−f(3)}+{f(3)−f(4)} +{f(4)−f(5)}+...+{f(n−1)−f(n)}+{f(n)−f(n+1)} S=f(1)−f(n+1) S=(1/(1!))−(1/((n+1)!))=1−(1/((n+1)!)) Corollary: lim_(n→∞) S=1−0=1](https://www.tinkutara.com/question/Q8556.png)
$$\mathrm{S}=\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{r}}{\left(\mathrm{r}+\mathrm{1}\right)!}=\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left[\frac{\mathrm{1}}{\mathrm{r}!}−\frac{\mathrm{1}}{\left(\mathrm{r}+\mathrm{1}\right)!}\right]=\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left\{\mathrm{f}\left(\mathrm{r}\right)−\mathrm{f}\left(\mathrm{r}+\mathrm{1}\right)\right\} \\ $$$$\mathrm{S}=\left\{\mathrm{f}\left(\mathrm{1}\right)−\mathrm{f}\left(\mathrm{2}\right)\right\}+\left\{\mathrm{f}\left(\mathrm{2}\right)−\mathrm{f}\left(\mathrm{3}\right)\right\}+\left\{\mathrm{f}\left(\mathrm{3}\right)−\mathrm{f}\left(\mathrm{4}\right)\right\} \\ $$$$+\left\{\mathrm{f}\left(\mathrm{4}\right)−\mathrm{f}\left(\mathrm{5}\right)\right\}+…+\left\{\mathrm{f}\left(\mathrm{n}−\mathrm{1}\right)−\mathrm{f}\left(\mathrm{n}\right)\right\}+\left\{\mathrm{f}\left(\mathrm{n}\right)−\mathrm{f}\left(\mathrm{n}+\mathrm{1}\right)\right\} \\ $$$$\mathrm{S}=\mathrm{f}\left(\mathrm{1}\right)−\mathrm{f}\left(\mathrm{n}+\mathrm{1}\right) \\ $$$$\mathrm{S}=\frac{\mathrm{1}}{\mathrm{1}!}−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!}=\mathrm{1}−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!} \\ $$$$\mathrm{Corollary}:\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}S}=\mathrm{1}−\mathrm{0}=\mathrm{1} \\ $$
