Question Number 67373 by mathmax by abdo last updated on 26/Aug/19
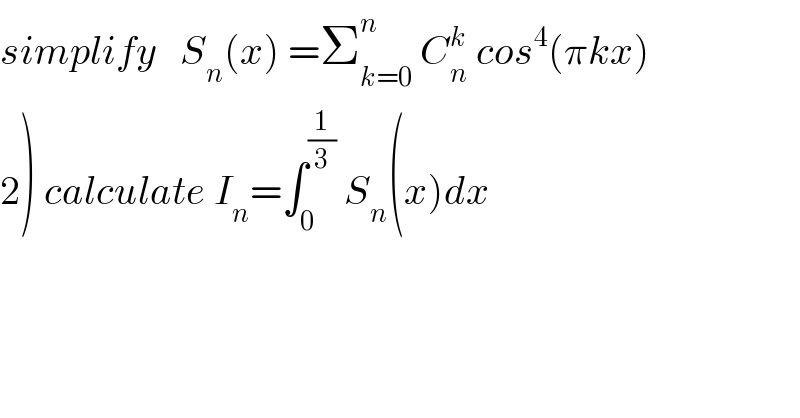
$${simplify}\:\:\:{S}_{{n}} \left({x}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}^{\mathrm{4}} \left(\pi{kx}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{I}_{{n}} =\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:{S}_{{n}} \left({x}\right){dx} \\ $$
Commented by ~ À ® @ 237 ~ last updated on 27/Aug/19
![Let state T_n =Σ_(k=0) ^n C_n ^k sin^4 (πkx) knowing that cos^4 t+sin^4 t=1−((sin^2 2t)/2) =((3+cos4t)/4) and cos^2 t −sin^2 t=cos2t S_n +T_n =(3/4)Σ_(k=0) ^n C_n ^k + (1/4)Σ_(k=0) ^n C_n ^k cos(4πkx)=3.2^(n−2) +(1/4)Re(Σ_(k=0) ^n C_n ^k (e^(i4πx) )^k )=3.2^(n−2) +(1/4)Re[(1+e^(i4πx) )^n ] =3.2^(n−2) +(1/4) Re[e^(i2πnx) (e^(i2πx) +e^(−i2πx) )^n ]=3.2^(n−2) + 2^(n−2) cos(2πnx)(cos(2πx)^n S_n −T_n = Σ_(k=0) ^n C_n ^k cos(2πkx)= Re[(1+e^(i2πx) )^n ]=2^n cos(nπx)(cos(πx))^n Now we can deduce S_n = 2^(n−3) [ 3 +cos(2πnx)(cos(2πx))^n +4cos(nπx)(cos(πx))^n ] But if we are searching a lowest form in the way to find I we can use cos^4 t= ((3+cos4t)/8) +((cos2t)/2) I_n = (1/3)+Σ_(k=1) ^n C_n ^k ∫_0 ^(1/3) [(3/8) +((cos(4πkx))/8) +((cos(2πkx))/2)]dx = (1/3)+Σ_(k=1) ^n C_(n ) ^k [ ((3x)/8) + ((sin(4πkx))/(32πk)) +((sin(2πkx))/(4πk))]_0 ^(1/3) = ((1/3)−(1/8))+(1/8)Σ_(k=0) ^n C_n ^k + (1/(32π)) Σ_(k=1) ^n C_n ^k ((sin(((4πk)/3)))/k) +(1/(4π))Σ_(k=1) ^n C_n ^k ((sin(((2πk)/3)))/k)](https://www.tinkutara.com/question/Q67424.png)
$$ \\ $$$$ \\ $$$${Let}\:{state}\:{T}_{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} \:{sin}^{\mathrm{4}} \left(\pi{kx}\right) \\ $$$${knowing}\:{that}\:\:{cos}^{\mathrm{4}} {t}+{sin}^{\mathrm{4}} {t}=\mathrm{1}−\frac{{sin}^{\mathrm{2}} \mathrm{2}{t}}{\mathrm{2}}\:=\frac{\mathrm{3}+{cos}\mathrm{4}{t}}{\mathrm{4}}\:\:{and}\:{cos}^{\mathrm{2}} {t}\:−{sin}^{\mathrm{2}} {t}={cos}\mathrm{2}{t} \\ $$$${S}_{{n}} +{T}_{{n}} =\frac{\mathrm{3}}{\mathrm{4}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} \:{cos}\left(\mathrm{4}\pi{kx}\right)=\mathrm{3}.\mathrm{2}^{{n}−\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}{Re}\left(\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} \:\left({e}^{{i}\mathrm{4}\pi{x}} \right)^{{k}} \right)=\mathrm{3}.\mathrm{2}^{{n}−\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}{Re}\left[\left(\mathrm{1}+{e}^{{i}\mathrm{4}\pi{x}} \right)^{{n}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}.\mathrm{2}^{{n}−\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}\:{Re}\left[{e}^{{i}\mathrm{2}\pi{nx}} \left({e}^{{i}\mathrm{2}\pi{x}} +{e}^{−{i}\mathrm{2}\pi{x}} \right)^{{n}} \right]=\mathrm{3}.\mathrm{2}^{{n}−\mathrm{2}} +\:\mathrm{2}^{{n}−\mathrm{2}} {cos}\left(\mathrm{2}\pi{nx}\right)\left({cos}\left(\mathrm{2}\pi{x}\right)^{{n}} \:\right. \\ $$$${S}_{{n}} −{T}_{{n}} =\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} \:{cos}\left(\mathrm{2}\pi{kx}\right)=\:{Re}\left[\left(\mathrm{1}+{e}^{{i}\mathrm{2}\pi{x}} \right)^{{n}} \right]=\mathrm{2}^{{n}} {cos}\left({n}\pi{x}\right)\left({cos}\left(\pi{x}\right)\right)^{{n}} \\ $$$${Now}\:{we}\:{can}\:{deduce}\: \\ $$$${S}_{{n}} =\:\mathrm{2}^{{n}−\mathrm{3}} \left[\:\mathrm{3}\:+{cos}\left(\mathrm{2}\pi{nx}\right)\left({cos}\left(\mathrm{2}\pi{x}\right)\right)^{{n}} +\mathrm{4}{cos}\left({n}\pi{x}\right)\left({cos}\left(\pi{x}\right)\right)^{{n}} \right]\: \\ $$$${But}\:{if}\:{we}\:{are}\:{searching}\:{a}\:{lowest}\:{form}\:{in}\:{the}\:{way}\:{to}\:{find}\:{I} \\ $$$${we}\:{can}\:{use}\:\:{cos}^{\mathrm{4}} {t}=\:\frac{\mathrm{3}+{cos}\mathrm{4}{t}}{\mathrm{8}}\:+\frac{{cos}\mathrm{2}{t}}{\mathrm{2}}\: \\ $$$${I}_{{n}} =\:\:\frac{\mathrm{1}}{\mathrm{3}}+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:{C}_{{n}} ^{{k}} \:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:\left[\frac{\mathrm{3}}{\mathrm{8}}\:+\frac{{cos}\left(\mathrm{4}\pi{kx}\right)}{\mathrm{8}}\:+\frac{{cos}\left(\mathrm{2}\pi{kx}\right)}{\mathrm{2}}\right]{dx} \\ $$$$\:\:\:=\:\:\frac{\mathrm{1}}{\mathrm{3}}+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:{C}_{{n}\:} ^{{k}} \left[\:\frac{\mathrm{3}{x}}{\mathrm{8}}\:+\:\frac{{sin}\left(\mathrm{4}\pi{kx}\right)}{\mathrm{32}\pi{k}}\:+\frac{{sin}\left(\mathrm{2}\pi{kx}\right)}{\mathrm{4}\pi{k}}\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \: \\ $$$$\:=\:\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{8}}\right)+\frac{\mathrm{1}}{\mathrm{8}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\:{C}_{{n}} ^{{k}} \:+\:\frac{\mathrm{1}}{\mathrm{32}\pi}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:{C}_{{n}} ^{{k}} \:\frac{{sin}\left(\frac{\mathrm{4}\pi{k}}{\mathrm{3}}\right)}{{k}}\:+\frac{\mathrm{1}}{\mathrm{4}\pi}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} \:\frac{{sin}\left(\frac{\mathrm{2}\pi{k}}{\mathrm{3}}\right)}{{k}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by mathmax by abdo last updated on 27/Aug/19

$${thank}\:{you}\:{sir}. \\ $$
Commented by mathmax by abdo last updated on 27/Aug/19

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{cos}^{\mathrm{4}} {u}\:=\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{u}\right.}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}{u}\right)+\frac{\mathrm{1}+{cos}\left(\mathrm{4}{u}\right)}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left\{\mathrm{2}+\mathrm{4}{cos}\left(\mathrm{2}{u}\right)\:+\mathrm{1}+{cos}\left(\mathrm{4}{u}\right)\right\}\:=\frac{\mathrm{1}}{\mathrm{8}}\left\{\mathrm{3}\:+\mathrm{4}{cos}\left(\mathrm{2}{u}\right)+{cos}\left(\mathrm{4}{u}\right)\right\} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\mathrm{2}{u}\right)+\frac{\mathrm{1}}{\mathrm{8}}{cos}\left(\mathrm{4}{u}\right)\:\Rightarrow \\ $$$${S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left\{\frac{\mathrm{3}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\mathrm{2}\pi{kx}\right)+\frac{\mathrm{1}}{\mathrm{8}}{cos}\left(\mathrm{4}\pi{kx}\right)\right\} \\ $$$$\left.=\frac{\mathrm{3}}{\mathrm{8}}×\mathrm{2}^{{n}} \:+\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}\left(\mathrm{2}\pi{kx}\right)\:+\frac{\mathrm{1}}{\mathrm{8}}\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}\left(\mathrm{4}\pi{kx}\right)\right\} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}\left(\mathrm{2}\pi{kx}\right)\:={Re}\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{e}^{{i}\mathrm{2}\pi{kx}} \right)\:{and} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left({e}^{{i}\mathrm{2}\pi{x}} \right)^{{k}} \:=\left(\mathrm{1}+{e}^{{i}\mathrm{2}\pi{x}} \right)^{{n}} =\left(\mathrm{1}+{cos}\left(\mathrm{2}\pi{x}\right)+{isin}\left(\mathrm{2}\pi{x}\right)\right)^{{n}} \\ $$$$\mid\mathrm{1}+{cos}\left(\mathrm{2}\pi{x}\right)+{isin}\left(\mathrm{2}\pi{x}\right)\mid\:=\sqrt{\left(\mathrm{1}+{cos}\left(\mathrm{2}\pi{x}\right)\right)^{\mathrm{2}} +\:{sin}^{\mathrm{2}} \left(\mathrm{2}\pi{x}\right)} \\ $$$$=\sqrt{\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}\pi{x}\right)+\mathrm{1}}=\sqrt{\mathrm{2}+\mathrm{2}{cos}\left(\mathrm{2}\pi{x}\right)}=\sqrt{\mathrm{2}}\sqrt{\mathrm{2}{cos}^{\mathrm{2}} \left(\pi{x}\right)} \\ $$$$=\mathrm{2}\mid{cos}\left(\pi{x}\right)\mid\:\Rightarrow \\ $$$$\mathrm{1}+{cos}\left(\mathrm{2}\pi{x}\right)+{isin}\left(\mathrm{2}\pi{x}\right)\:=\mathrm{2}\mid{cos}\left(\pi{x}\right)\mid\:{e}^{{i}\:{arctan}\left(\frac{{sin}\left(\mathrm{2}\pi{x}\right)}{\mathrm{1}+{cos}\left(\mathrm{2}\pi{x}\right)}\right)} \:=\mathrm{2}\mid{cos}\left(\pi{x}\right)\mid{e}^{{i}\pi{x}} \:{because} \\ $$$$\frac{{sin}\left(\mathrm{2}\pi{x}\right)}{\mathrm{1}+{cos}\left(\mathrm{2}\pi{x}\right)}\:=\frac{\mathrm{2}{sin}\left(\pi{x}\right){cos}\left(\pi{x}\right)}{\mathrm{2}{cos}^{\mathrm{2}} \left(\pi{x}\right)}\:={tan}\left(\pi{x}\right)\:\Rightarrow \\ $$$$\left(\mathrm{1}+{cos}\left(\mathrm{2}\pi{x}\right)+{isin}\left(\mathrm{2}\pi{x}\right)\right)^{{n}} \:=\mathrm{2}^{{n}} \mid{cos}\left(\pi{x}\right)\mid^{{n}} \:{e}^{{in}\pi{x}} \:{also}\:{we}\:{have} \\ $$$$\Rightarrow\sum_{{k}=\mathrm{0}} ^{{n}\:\:} \:{C}_{{n}} ^{{k}} \:{cos}\left(\mathrm{2}\pi{kx}\right)\:=\mathrm{2}^{{n}} \mid{cos}\left(\pi{x}\right)\mid^{{n}} \:{cos}\left({n}\pi{x}\right)\:{also} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}\left(\mathrm{4}\pi{kx}\right)\:=\mathrm{2}^{{n}} \mid{cos}\left(\mathrm{2}\pi{x}\right)\mid^{{n}} \:{cos}\left(\mathrm{2}{n}\pi{x}\right)\:\Rightarrow \\ $$$${S}_{{n}} =\frac{\mathrm{3}×\mathrm{2}^{{n}} }{\mathrm{8}}\:+\:\mathrm{2}^{{n}−\mathrm{1}} \mid{cos}\left(\pi{x}\right)\mid^{{n}} \:{cos}\left({n}\pi{x}\right)\:+\mathrm{2}^{{n}−\mathrm{3}} \:\mid{cos}\left(\mathrm{2}\pi{x}\right)\mid^{{n}} \:{cos}\left(\mathrm{2}{n}\pi{x}\right) \\ $$
Commented by mathmax by abdo last updated on 27/Aug/19
![2) ∫_0 ^(1/3) S(x)dx =∫_0 ^(1/3) {(3/8)2^n +(1/2)Σ_(k=0) ^n C_n ^k cos(2πkx)+(1/8)Σ_(k=0) ^n C_n ^k cos(4πkx)}dx =2^(n−3) +(1/2)Σ_(k=0) ^n ∫_0 ^(1/3) cos(2πkx)dx +(1/8)Σ_(k=0) ^n C_n ^k ∫_0 ^(1/3) cos(4πkx)dx =2^(n−3) +(1/2)Σ_(k=0) ^n (1/(2πk))[sin(2πkx]_0 ^(1/3) +(1/8)Σ_(k=0) ^n C_n ^k (1/(4πk))[sin(4πkx)]_0 ^(1/3) =2^(n−3) + (1/(4π)) Σ_(k=0) ^n ((sin(((2πk)/3)))/k) +(1/(32π))Σ_(k=0) ^n C_n ^k ((sin(((4πk)/3)))/k) .](https://www.tinkutara.com/question/Q67442.png)
$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:{S}\left({x}\right){dx}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \left\{\frac{\mathrm{3}}{\mathrm{8}}\mathrm{2}^{{n}} \:+\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}\left(\mathrm{2}\pi{kx}\right)+\frac{\mathrm{1}}{\mathrm{8}}\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}\left(\mathrm{4}\pi{kx}\right)\right\}{dx} \\ $$$$=\mathrm{2}^{{n}−\mathrm{3}} \:+\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{0}} ^{{n}} \:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:{cos}\left(\mathrm{2}\pi{kx}\right){dx}\:+\frac{\mathrm{1}}{\mathrm{8}}\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:{cos}\left(\mathrm{4}\pi{kx}\right){dx} \\ $$$$=\mathrm{2}^{{n}−\mathrm{3}} \:+\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{0}} ^{{n}} \frac{\mathrm{1}}{\mathrm{2}\pi{k}}\left[{sin}\left(\mathrm{2}\pi{kx}\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:+\frac{\mathrm{1}}{\mathrm{8}}\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\:\frac{\mathrm{1}}{\mathrm{4}\pi{k}}\left[{sin}\left(\mathrm{4}\pi{kx}\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \right. \\ $$$$=\mathrm{2}^{{n}−\mathrm{3}} \:+\:\frac{\mathrm{1}}{\mathrm{4}\pi}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\frac{{sin}\left(\frac{\mathrm{2}\pi{k}}{\mathrm{3}}\right)}{{k}}\:+\frac{\mathrm{1}}{\mathrm{32}\pi}\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\frac{{sin}\left(\frac{\mathrm{4}\pi{k}}{\mathrm{3}}\right)}{{k}}\:. \\ $$
Answered by Smail last updated on 27/Aug/19
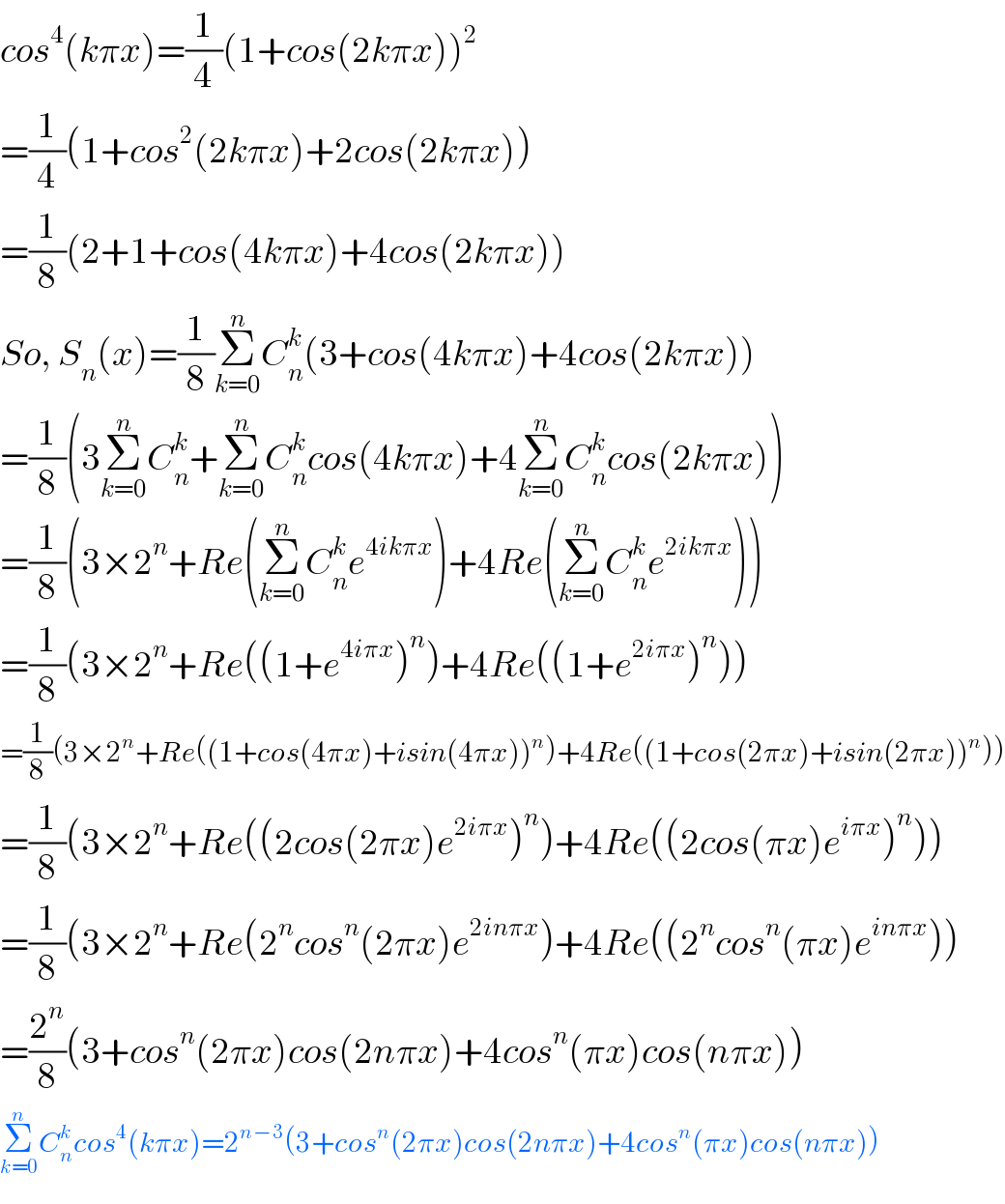
$${cos}^{\mathrm{4}} \left({k}\pi{x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+{cos}\left(\mathrm{2}{k}\pi{x}\right)\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+{cos}^{\mathrm{2}} \left(\mathrm{2}{k}\pi{x}\right)+\mathrm{2}{cos}\left(\mathrm{2}{k}\pi{x}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{2}+\mathrm{1}+{cos}\left(\mathrm{4}{k}\pi{x}\right)+\mathrm{4}{cos}\left(\mathrm{2}{k}\pi{x}\right)\right) \\ $$$${So},\:{S}_{{n}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{8}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} \left(\mathrm{3}+{cos}\left(\mathrm{4}{k}\pi{x}\right)+\mathrm{4}{cos}\left(\mathrm{2}{k}\pi{x}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{3}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} +\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} {cos}\left(\mathrm{4}{k}\pi{x}\right)+\mathrm{4}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} {cos}\left(\mathrm{2}{k}\pi{x}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{3}×\mathrm{2}^{{n}} +{Re}\left(\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} {e}^{\mathrm{4}{ik}\pi{x}} \right)+\mathrm{4}{Re}\left(\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} {e}^{\mathrm{2}{ik}\pi{x}} \right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{3}×\mathrm{2}^{{n}} +{Re}\left(\left(\mathrm{1}+{e}^{\mathrm{4}{i}\pi{x}} \right)^{{n}} \right)+\mathrm{4}{Re}\left(\left(\mathrm{1}+{e}^{\mathrm{2}{i}\pi{x}} \right)^{{n}} \right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{3}×\mathrm{2}^{{n}} +{Re}\left(\left(\mathrm{1}+{cos}\left(\mathrm{4}\pi{x}\right)+{isin}\left(\mathrm{4}\pi{x}\right)\right)^{{n}} \right)+\mathrm{4}{Re}\left(\left(\mathrm{1}+{cos}\left(\mathrm{2}\pi{x}\right)+{isin}\left(\mathrm{2}\pi{x}\right)\right)^{{n}} \right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{3}×\mathrm{2}^{{n}} +{Re}\left(\left(\mathrm{2}{cos}\left(\mathrm{2}\pi{x}\right){e}^{\mathrm{2}{i}\pi{x}} \right)^{{n}} \right)+\mathrm{4}{Re}\left(\left(\mathrm{2}{cos}\left(\pi{x}\right){e}^{{i}\pi{x}} \right)^{{n}} \right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{3}×\mathrm{2}^{{n}} +{Re}\left(\mathrm{2}^{{n}} {cos}^{{n}} \left(\mathrm{2}\pi{x}\right){e}^{\mathrm{2}{in}\pi{x}} \right)+\mathrm{4}{Re}\left(\left(\mathrm{2}^{{n}} {cos}^{{n}} \left(\pi{x}\right){e}^{{in}\pi{x}} \right)\right)\right. \\ $$$$=\frac{\mathrm{2}^{{n}} }{\mathrm{8}}\left(\mathrm{3}+{cos}^{{n}} \left(\mathrm{2}\pi{x}\right){cos}\left(\mathrm{2}{n}\pi{x}\right)+\mathrm{4}{cos}^{{n}} \left(\pi{x}\right){cos}\left({n}\pi{x}\right)\right) \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} {cos}^{\mathrm{4}} \left({k}\pi{x}\right)=\mathrm{2}^{{n}−\mathrm{3}} \left(\mathrm{3}+{cos}^{{n}} \left(\mathrm{2}\pi{x}\right){cos}\left(\mathrm{2}{n}\pi{x}\right)+\mathrm{4}{cos}^{{n}} \left(\pi{x}\right){cos}\left({n}\pi{x}\right)\right) \\ $$
