Question Number 6317 by sanusihammed last updated on 23/Jun/16

$${Solve}\:{the}\:{system}\:{of}\:{equation}\: \\ $$$$ \\ $$$${x}\:+\:{y}\:−\:{z}\:=\:\mathrm{9}\:\:\:……….\:{equation}\:\left({i}\right) \\ $$$${x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}\:} +\:{z}^{\mathrm{2}\:} =\:\mathrm{99}\:\:………..\:{equation}\:\left({ii}\right) \\ $$$${y}^{\mathrm{2}} \:=\:{xz}\:\:\:………..\:{equation}\left({iii}\right) \\ $$
Commented by prakash jain last updated on 23/Jun/16
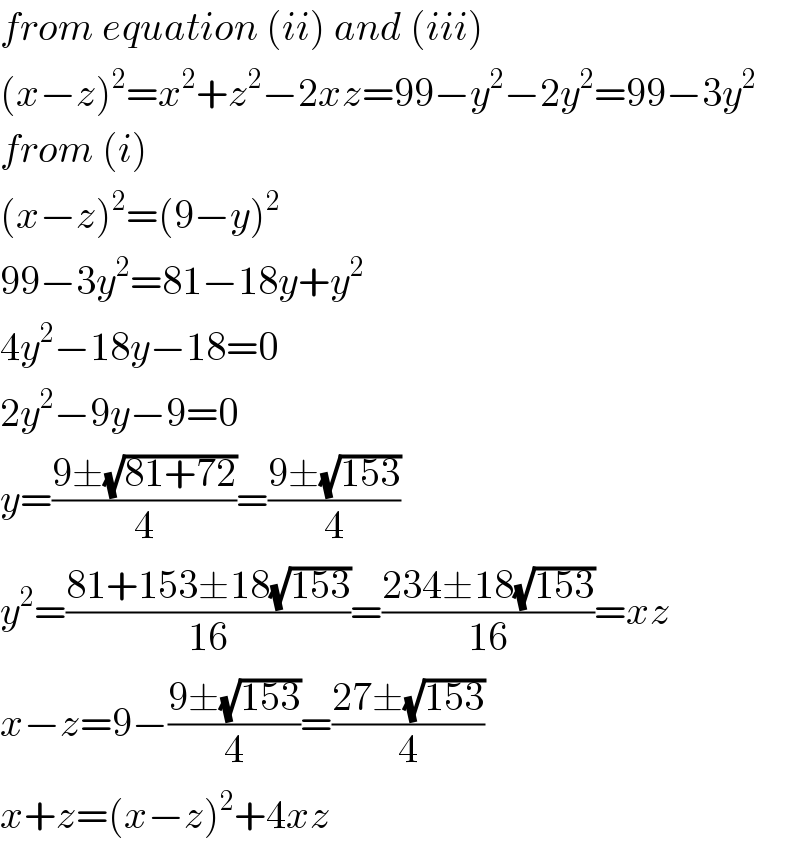
$${from}\:{equation}\:\left({ii}\right)\:{and}\:\left({iii}\right) \\ $$$$\left({x}−{z}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} +{z}^{\mathrm{2}} −\mathrm{2}{xz}=\mathrm{99}−{y}^{\mathrm{2}} −\mathrm{2}{y}^{\mathrm{2}} =\mathrm{99}−\mathrm{3}{y}^{\mathrm{2}} \\ $$$${from}\:\left({i}\right) \\ $$$$\left({x}−{z}\right)^{\mathrm{2}} =\left(\mathrm{9}−{y}\right)^{\mathrm{2}} \\ $$$$\mathrm{99}−\mathrm{3}{y}^{\mathrm{2}} =\mathrm{81}−\mathrm{18}{y}+{y}^{\mathrm{2}} \\ $$$$\mathrm{4}{y}^{\mathrm{2}} −\mathrm{18}{y}−\mathrm{18}=\mathrm{0} \\ $$$$\mathrm{2}{y}^{\mathrm{2}} −\mathrm{9}{y}−\mathrm{9}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{9}\pm\sqrt{\mathrm{81}+\mathrm{72}}}{\mathrm{4}}=\frac{\mathrm{9}\pm\sqrt{\mathrm{153}}}{\mathrm{4}} \\ $$$${y}^{\mathrm{2}} =\frac{\mathrm{81}+\mathrm{153}\pm\mathrm{18}\sqrt{\mathrm{153}}}{\mathrm{16}}=\frac{\mathrm{234}\pm\mathrm{18}\sqrt{\mathrm{153}}}{\mathrm{16}}={xz} \\ $$$${x}−{z}=\mathrm{9}−\frac{\mathrm{9}\pm\sqrt{\mathrm{153}}}{\mathrm{4}}=\frac{\mathrm{27}\pm\sqrt{\mathrm{153}}}{\mathrm{4}} \\ $$$${x}+{z}=\left({x}−{z}\right)^{\mathrm{2}} +\mathrm{4}{xz} \\ $$
Answered by Rasheed Soomro last updated on 24/Jun/16
![x + y − z = 9 ............... (i) x^2 + y^(2 ) + z^(2 ) = 99 ........... (ii) y^2 = xz ........... .............(iii) (i)^2 : (x + y − z)^2 = 9^2 x^2 + y^(2 ) + z^(2 ) +2xy−2yz−2zx=81 99+2xy−2yz−2(y^2 )=81 [ (ii)x^2 + y^(2 ) + z^(2 ) = 99 & (iii)xz=y^2 ] 2xy−2yz−2y^2 =−18 xy−yz−y^2 =−9 y(x−z^(−) −y)=−9 y(9−y−y)=−9 [From(i) x−z=9−y] 9y−2y^2 =−9 2y^2 −9y−9=0 y=((9±(√(81+72)))/4)=((9±(√(153)))/4)= continue](https://www.tinkutara.com/question/Q6336.png)
$${x}\:+\:{y}\:−\:{z}\:=\:\mathrm{9}\:\:\:……………\:\left({i}\right) \\ $$$${x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}\:} +\:{z}^{\mathrm{2}\:} =\:\mathrm{99}\:\:………..\:\:\left({ii}\right) \\ $$$${y}^{\mathrm{2}} \:=\:{xz}\:\:\:………..\:………….\left({iii}\right) \\ $$$$\left({i}\right)^{\mathrm{2}} \::\:\left({x}\:+\:{y}\:−\:{z}\right)^{\mathrm{2}} \:=\:\mathrm{9}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}\:} +\:{z}^{\mathrm{2}\:} +\mathrm{2}{xy}−\mathrm{2}{yz}−\mathrm{2}{zx}=\mathrm{81} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{99}+\mathrm{2}{xy}−\mathrm{2}{yz}−\mathrm{2}\left({y}^{\mathrm{2}} \right)=\mathrm{81}\:\:\left[\:\left({ii}\right){x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}\:} +\:{z}^{\mathrm{2}\:} =\:\mathrm{99}\:\&\:\left({iii}\right){xz}={y}^{\mathrm{2}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{2}{xy}−\mathrm{2}{yz}−\mathrm{2}{y}^{\mathrm{2}} =−\mathrm{18} \\ $$$$\:\:\:\:\:\:\:\:\:{xy}−{yz}−{y}^{\mathrm{2}} =−\mathrm{9} \\ $$$${y}\left(\overline {{x}−{z}}−{y}\right)=−\mathrm{9} \\ $$$${y}\left(\mathrm{9}−{y}−{y}\right)=−\mathrm{9}\:\:\:\left[{From}\left({i}\right)\:{x}−{z}=\mathrm{9}−{y}\right] \\ $$$$\mathrm{9}{y}−\mathrm{2}{y}^{\mathrm{2}} =−\mathrm{9} \\ $$$$\mathrm{2}{y}^{\mathrm{2}} −\mathrm{9}{y}−\mathrm{9}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{9}\pm\sqrt{\mathrm{81}+\mathrm{72}}}{\mathrm{4}}=\frac{\mathrm{9}\pm\sqrt{\mathrm{153}}}{\mathrm{4}}= \\ $$$$ \\ $$$${continue} \\ $$
Commented by Rasheed Soomro last updated on 24/Jun/16

$${A}\:{defferent}\:\:{way}\:\:{to}\:{determine}\:{value}\:{of}\:{y}\:{in}\: \\ $$$${the}\:{question}.\:{Don}'{t}\:{claim}\:{to}\:{be}\:{better}\:{than} \\ $$$${the}\:{way}\:{in}\:{comment}\:{by}\:{sir}\:{prakash}\:{above}. \\ $$
