Question Number 7142 by Tawakalitu. last updated on 13/Aug/16
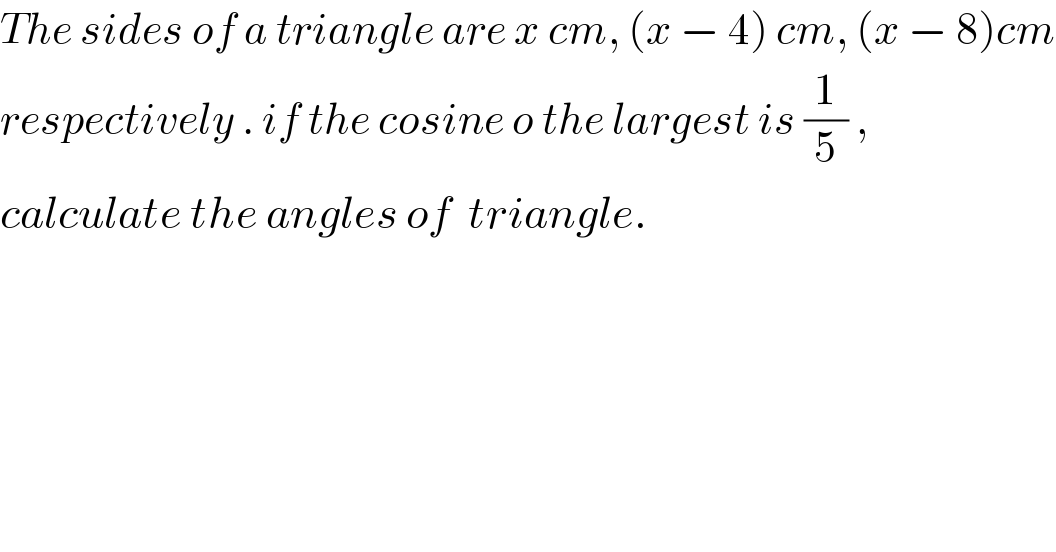
$${The}\:{sides}\:{of}\:{a}\:{triangle}\:{are}\:{x}\:{cm},\:\left({x}\:−\:\mathrm{4}\right)\:{cm},\:\left({x}\:−\:\mathrm{8}\right){cm} \\ $$$${respectively}\:.\:{if}\:{the}\:{cosine}\:{o}\:{the}\:{largest}\:{is}\:\frac{\mathrm{1}}{\mathrm{5}}\:,\: \\ $$$${calculate}\:{the}\:{angles}\:{of}\:\:{triangle}. \\ $$$$ \\ $$
Answered by Rasheed Soomro last updated on 13/Aug/16
![∵ x , x−4 , x−8 >0 [measures of the sides must be positive] ∴ x >8 and it′s the largest. Let the opposite angle to the largest side(whose measure is x) is α.According to cosine law: x^2 =(x−4)^2 +(x−8)^2 −2(x−4)(x−8)cos α x^2 =(x−4)^2 +(x−8)^2 −2(x−4)(x−8)((1/5)) [∵cos α=(1/5)] 5x^2 =5x^2 −40x+80+5x^2 −80x+320−2x^2 +24x−64 −40x+80+5x^2 −80x+320−2x^2 +24x−64=0 3x^2 −96x+336=0 x^2 −32x+112=0 x=((32±(√(1024−448)))/2)=((32±(√(576)))/2)=((32±24)/2)=16±12 x=28 ∣ x=4 x=4 is discardable since x>8 [x=4 makes the sides of triangle 0 and negative] So, x=28 , x−4=24 and x=20 I-e the sides of the triangle are 28,24 and 20 Let α,β and γ are oppsite angles of the sides having measures 28,24 and 20 respectively. cos α=((20^2 +24^2 −28^2 )/(2×20×24))=(1/5)⇒α=cos^(−1) (1/5)≈78.46° cos β=((20^2 +28^2 −24^2 )/(2×20×28))=((19)/(35))⇒β=cos^(−1) ((19)/(35))≈57.12° cos β=((24^2 +28^2 −20^2 )/(2×24×28))=(5/7)⇒β=cos^(−1) (5/7)≈44.42°](https://www.tinkutara.com/question/Q7144.png)
$$\because\:{x}\:,\:{x}−\mathrm{4}\:,\:{x}−\mathrm{8}\:>\mathrm{0}\:\:\:\left[{measures}\:{of}\:{the}\:{sides}\:{must}\:{be}\:\:{positive}\right] \\ $$$$\therefore\:{x}\:>\mathrm{8}\:{and}\:{it}'{s}\:{the}\:{largest}. \\ $$$${Let}\:{the}\:\:{opposite}\:{angle}\:{to}\:{the}\:{largest}\:{side}\left({whose}\right. \\ $$$$\left.{measure}\:{is}\:{x}\right)\:{is}\:\alpha.{According}\:{to}\:{cosine}\:{law}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} =\left({x}−\mathrm{4}\right)^{\mathrm{2}} +\left({x}−\mathrm{8}\right)^{\mathrm{2}} −\mathrm{2}\left({x}−\mathrm{4}\right)\left({x}−\mathrm{8}\right)\mathrm{cos}\:\alpha \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} =\left({x}−\mathrm{4}\right)^{\mathrm{2}} +\left({x}−\mathrm{8}\right)^{\mathrm{2}} −\mathrm{2}\left({x}−\mathrm{4}\right)\left({x}−\mathrm{8}\right)\left(\frac{\mathrm{1}}{\mathrm{5}}\right)\:\:\left[\because\mathrm{cos}\:\alpha=\frac{\mathrm{1}}{\mathrm{5}}\right] \\ $$$$\:\:\:\:\:\:\:\mathrm{5}{x}^{\mathrm{2}} =\mathrm{5}{x}^{\mathrm{2}} −\mathrm{40}{x}+\mathrm{80}+\mathrm{5}{x}^{\mathrm{2}} −\mathrm{80}{x}+\mathrm{320}−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{24}{x}−\mathrm{64} \\ $$$$\:\:\:\:\:\:\:−\mathrm{40}{x}+\mathrm{80}+\mathrm{5}{x}^{\mathrm{2}} −\mathrm{80}{x}+\mathrm{320}−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{24}{x}−\mathrm{64}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{3}{x}^{\mathrm{2}} −\mathrm{96}{x}+\mathrm{336}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{32}{x}+\mathrm{112}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:{x}=\frac{\mathrm{32}\pm\sqrt{\mathrm{1024}−\mathrm{448}}}{\mathrm{2}}=\frac{\mathrm{32}\pm\sqrt{\mathrm{576}}}{\mathrm{2}}=\frac{\mathrm{32}\pm\mathrm{24}}{\mathrm{2}}=\mathrm{16}\pm\mathrm{12} \\ $$$$\:\:\:\:\:\:\:{x}=\mathrm{28}\:\mid\:\:{x}=\mathrm{4} \\ $$$${x}=\mathrm{4}\:{is}\:{discardable}\:{since}\:{x}>\mathrm{8}\:\left[{x}=\mathrm{4}\:{makes}\:{the}\:{sides}\right. \\ $$$$\left.{of}\:{triangle}\:\mathrm{0}\:{and}\:{negative}\right] \\ $$$${So},\:\:{x}=\mathrm{28}\:,\:{x}−\mathrm{4}=\mathrm{24}\:{and}\:{x}=\mathrm{20} \\ $$$${I}-{e}\:{the}\:{sides}\:{of}\:{the}\:{triangle}\:{are}\:\mathrm{28},\mathrm{24}\:{and}\:\mathrm{20} \\ $$$$ \\ $$$${Let}\:\:\alpha,\beta\:\:{and}\:\:\gamma\:\:{are}\:{oppsite}\:{angles}\:\:{of}\:\:{the}\:{sides}\:{having} \\ $$$${measures}\:\:\mathrm{28},\mathrm{24}\:\:{and}\:\mathrm{20}\:{respectively}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\alpha=\frac{\mathrm{20}^{\mathrm{2}} +\mathrm{24}^{\mathrm{2}} −\mathrm{28}^{\mathrm{2}} }{\mathrm{2}×\mathrm{20}×\mathrm{24}}=\frac{\mathrm{1}}{\mathrm{5}}\Rightarrow\alpha=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{5}}\approx\mathrm{78}.\mathrm{46}° \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\beta=\frac{\mathrm{20}^{\mathrm{2}} +\mathrm{28}^{\mathrm{2}} −\mathrm{24}^{\mathrm{2}} }{\mathrm{2}×\mathrm{20}×\mathrm{28}}=\frac{\mathrm{19}}{\mathrm{35}}\Rightarrow\beta=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{19}}{\mathrm{35}}\approx\mathrm{57}.\mathrm{12}° \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\beta=\frac{\mathrm{24}^{\mathrm{2}} +\mathrm{28}^{\mathrm{2}} −\mathrm{20}^{\mathrm{2}} }{\mathrm{2}×\mathrm{24}×\mathrm{28}}=\frac{\mathrm{5}}{\mathrm{7}}\Rightarrow\beta=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{5}}{\mathrm{7}}\approx\mathrm{44}.\mathrm{42}° \\ $$$$ \\ $$$$\:\:\:\:\:\:\: \\ $$
Commented by Tawakalitu. last updated on 13/Aug/16
$${Thank}\:{you}\:{so}\:{much}\:{sir}. \\ $$$$ \\ $$
