Question Number 70818 by oyemi kemewari last updated on 08/Oct/19
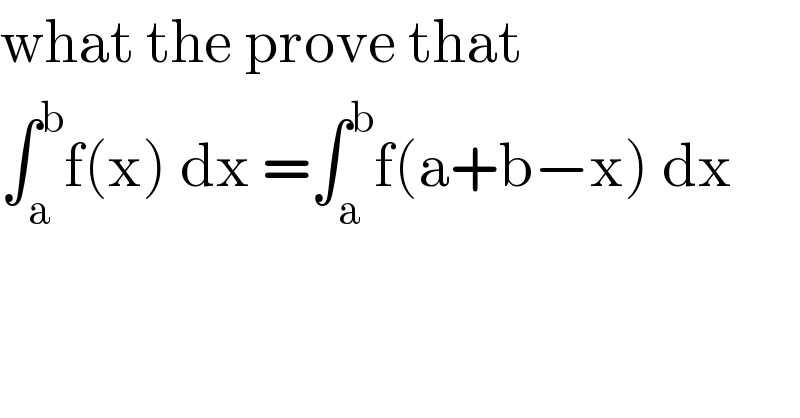
$$\mathrm{what}\:\mathrm{the}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{f}\left(\mathrm{x}\right)\:\mathrm{dx}\:=\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{f}\left(\mathrm{a}+\mathrm{b}−\mathrm{x}\right)\:\mathrm{dx} \\ $$
Commented by kaivan.ahmadi last updated on 08/Oct/19
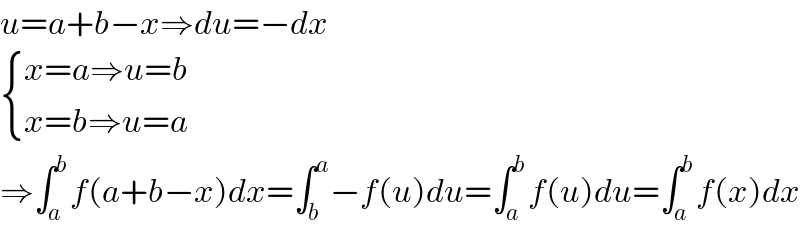
$${u}={a}+{b}−{x}\Rightarrow{du}=−{dx} \\ $$$$\begin{cases}{{x}={a}\Rightarrow{u}={b}}\\{{x}={b}\Rightarrow{u}={a}}\end{cases} \\ $$$$\Rightarrow\int_{{a}} ^{{b}} {f}\left({a}+{b}−{x}\right){dx}=\int_{{b}} ^{{a}} −{f}\left({u}\right){du}=\int_{{a}} ^{{b}} {f}\left({u}\right){du}=\int_{{a}} ^{{b}} {f}\left({x}\right){dx} \\ $$
Answered by MJS last updated on 08/Oct/19
![∫_a ^b f(x)dx=[F(x)]_a ^b =F(b)−F(a) ∫_a ^b f(a+b−x)dx= [t=a+b−x ⇒ dx=−dt] =−∫_b ^a f(t)dt=−[F(t)]_b ^a =[F(t)]_a ^b =F(b)−F(a)](https://www.tinkutara.com/question/Q70822.png)
$$\underset{{a}} {\overset{{b}} {\int}}{f}\left({x}\right){dx}=\left[{F}\left({x}\right)\right]_{{a}} ^{{b}} ={F}\left({b}\right)−{F}\left({a}\right) \\ $$$$\underset{{a}} {\overset{{b}} {\int}}{f}\left({a}+{b}−{x}\right){dx}= \\ $$$$\:\:\:\:\:\left[{t}={a}+{b}−{x}\:\Rightarrow\:{dx}=−{dt}\right] \\ $$$$=−\underset{{b}} {\overset{{a}} {\int}}{f}\left({t}\right){dt}=−\left[{F}\left({t}\right)\right]_{{b}} ^{{a}} =\left[{F}\left({t}\right)\right]_{{a}} ^{{b}} ={F}\left({b}\right)−{F}\left({a}\right) \\ $$
