Question Number 135646 by metamorfose last updated on 14/Mar/21
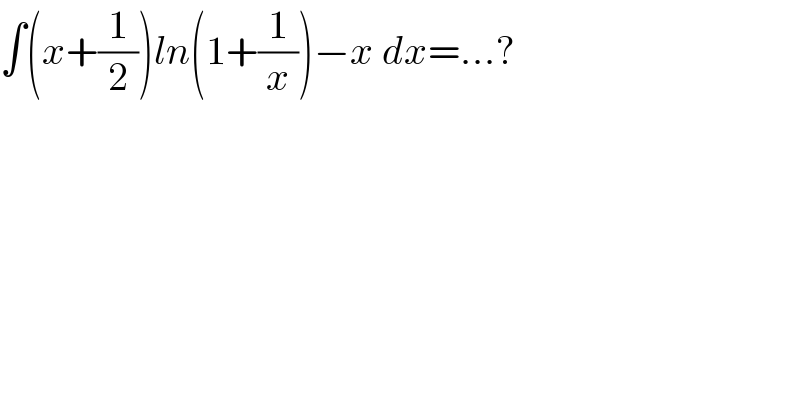
$$\int\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)−{x}\:{dx}=…? \\ $$
Answered by Ñï= last updated on 15/Mar/21
![∫[(x+(1/2))ln(1+(1/x))−x]dx =∫[(x+(1/2))(ln(x+1)−lnx)−x]dx =∫(x+(1/2))ln(x+1)dx−∫(x+(1/2))lnxdx−∫xdx =((1/2)x^2 +(1/2)x)ln(x+1)−∫((x+1−(1/2))/(x+1))dx−((1/2)x^2 +(1/2)x)lnx+∫((x+(1/2))/x)dx−(1/2)x^2 =((1/2)x^2 +(1/2)x)ln(1+(1/x))+(1/2)ln(x^2 +x)−(1/2)x^2 +C](https://www.tinkutara.com/question/Q135681.png)
$$\int\left[\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)−{x}\right]{dx} \\ $$$$=\int\left[\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({ln}\left({x}+\mathrm{1}\right)−{lnx}\right)−{x}\right]{dx} \\ $$$$=\int\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right){ln}\left({x}+\mathrm{1}\right){dx}−\int\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right){lnxdx}−\int{xdx} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{x}\right){ln}\left({x}+\mathrm{1}\right)−\int\frac{{x}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}{{x}+\mathrm{1}}{dx}−\left(\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{x}\right){lnx}+\int\frac{{x}+\frac{\mathrm{1}}{\mathrm{2}}}{{x}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{x}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} +{x}\right)−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{C} \\ $$
