Question Number 10101 by Tawakalitu ayo mi last updated on 23/Jan/17
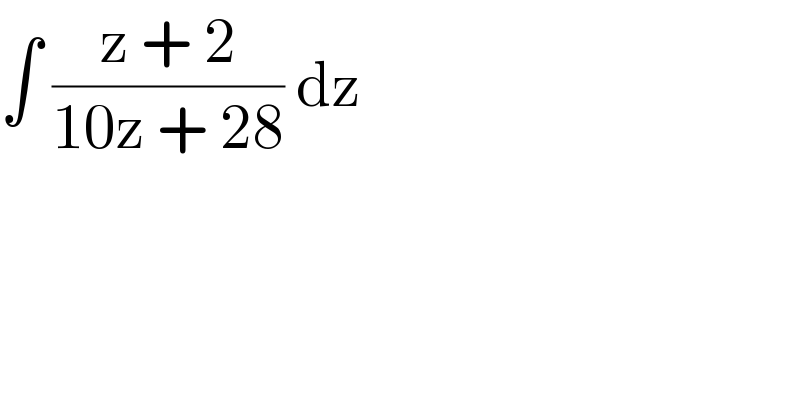
$$\int\:\frac{\mathrm{z}\:+\:\mathrm{2}}{\mathrm{10z}\:+\:\mathrm{28}}\:\mathrm{dz} \\ $$
Commented by prakash jain last updated on 24/Jan/17
![=(1/(10))∫((10z+28−8)/(10z+28))dz =(1/(10))∫[1−(8/(10z+28))]dz =(1/(10))[z−(8/(10))ln (10z+28)]+C](https://www.tinkutara.com/question/Q10109.png)
$$=\frac{\mathrm{1}}{\mathrm{10}}\int\frac{\mathrm{10}{z}+\mathrm{28}−\mathrm{8}}{\mathrm{10}{z}+\mathrm{28}}{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\int\left[\mathrm{1}−\frac{\mathrm{8}}{\mathrm{10}{z}+\mathrm{28}}\right]{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\left[{z}−\frac{\mathrm{8}}{\mathrm{10}}\mathrm{ln}\:\left(\mathrm{10}{z}+\mathrm{28}\right)\right]+{C} \\ $$
Commented by Tawakalitu ayo mi last updated on 24/Jan/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
