Question Number 164974 by mnjuly1970 last updated on 24/Jan/22
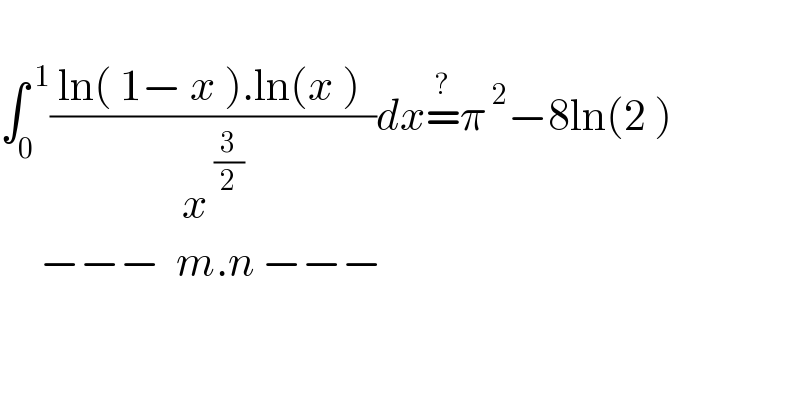
$$ \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\mathrm{ln}\left(\:\mathrm{1}−\:{x}\:\right).\mathrm{ln}\left({x}\:\right)\:\:}{{x}^{\:\frac{\mathrm{3}}{\mathrm{2}}} }{dx}\overset{?} {=}\pi^{\:\mathrm{2}} −\mathrm{8ln}\left(\mathrm{2}\:\right)\: \\ $$$$\:\:\:\:\:−−−\:\:{m}.{n}\:−−− \\ $$$$ \\ $$
Answered by qaz last updated on 24/Jan/22
![∫_0 ^1 ((ln(1−x)lnx)/x^(3/2) )dx =−Σ_(n=1) ^∞ (1/n)∫_0 ^1 x^(n−3/2) lnxdx =Σ_(n=1) ^∞ (1/(n(n−(1/2))^2 )) =Σ_(n=1) ^∞ [(4/n)−(4/(n−(1/2)))+(2/((n−(1/2))^2 ))] =4H_(−1/2) +8∙(1−2^(−2) )∙(π^2 /6) =−8ln2+π^2](https://www.tinkutara.com/question/Q164978.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{lnx}}{\mathrm{x}^{\mathrm{3}/\mathrm{2}} }\mathrm{dx} \\ $$$$=−\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{n}−\mathrm{3}/\mathrm{2}} \mathrm{lnxdx} \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{4}}{\mathrm{n}}−\frac{\mathrm{4}}{\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}}+\frac{\mathrm{2}}{\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\right] \\ $$$$=\mathrm{4H}_{−\mathrm{1}/\mathrm{2}} +\mathrm{8}\centerdot\left(\mathrm{1}−\mathrm{2}^{−\mathrm{2}} \right)\centerdot\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$=−\mathrm{8ln2}+\pi^{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 24/Jan/22
$$\:\:{thanks}\:{alot}\:{sir}\:{qaz} \\ $$
