Question Number 108664 by mohammad17 last updated on 18/Aug/20
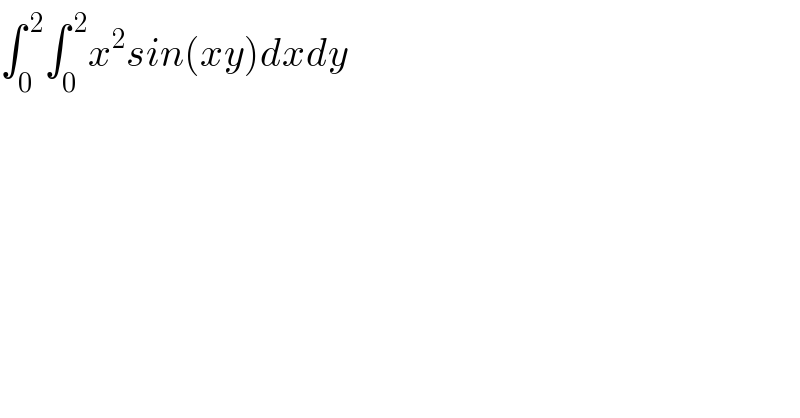
$$\int_{\mathrm{0}} ^{\:\mathrm{2}} \int_{\mathrm{0}} ^{\:\mathrm{2}} {x}^{\mathrm{2}} {sin}\left({xy}\right){dxdy} \\ $$
Answered by mathmax by abdo last updated on 18/Aug/20
![I =∫_0 ^2 ( ∫_0 ^2 sin(xy)dy)x^2 dx =∫_0 ^2 ([−(1/x)cos(xy)]_(y=0) ^(y=2) )x^2 dx =∫_0 ^2 x(1−cos(2x))dx =∫_0 ^2 xdx −∫_0 ^2 xcos(2x)dx =[(x^2 /2)]_0 ^2 −{ [(x/2)sin(2x)]_0 ^2 −∫_0 ^2 ((sin(2x))/2)dx} =2−{ sin(4)+(1/4)[cos(2x)]_0 ^2 } =2−{sin4 +(1/4)(cos4−1)) =2−sin4−(1/4)cos(4)+(1/4) =(9/4)−sin(4)−(1/4)cos(4)](https://www.tinkutara.com/question/Q108682.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \left(\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{xy}\right)\mathrm{dy}\right)\mathrm{x}^{\mathrm{2}} \mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \:\left(\left[−\frac{\mathrm{1}}{\mathrm{x}}\mathrm{cos}\left(\mathrm{xy}\right)\right]_{\mathrm{y}=\mathrm{0}} ^{\mathrm{y}=\mathrm{2}} \right)\mathrm{x}^{\mathrm{2}} \mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \:\mathrm{x}\left(\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)\right)\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \:\mathrm{xdx}\:−\int_{\mathrm{0}} ^{\mathrm{2}} \:\mathrm{xcos}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$=\left[\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{2}} \:−\left\{\:\:\left[\frac{\mathrm{x}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)\right]_{\mathrm{0}} ^{\mathrm{2}} −\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2}}\mathrm{dx}\right\} \\ $$$$=\mathrm{2}−\left\{\:\mathrm{sin}\left(\mathrm{4}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{cos}\left(\mathrm{2x}\right)\right]_{\mathrm{0}} ^{\mathrm{2}} \right\} \\ $$$$=\mathrm{2}−\left\{\mathrm{sin4}\:+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{cos4}−\mathrm{1}\right)\right)\:=\mathrm{2}−\mathrm{sin4}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\mathrm{4}\right)+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{9}}{\mathrm{4}}−\mathrm{sin}\left(\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\mathrm{4}\right) \\ $$
Commented by mohammad17 last updated on 18/Aug/20

$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 18/Aug/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
