Question Number 55237 by peter frank last updated on 19/Feb/19
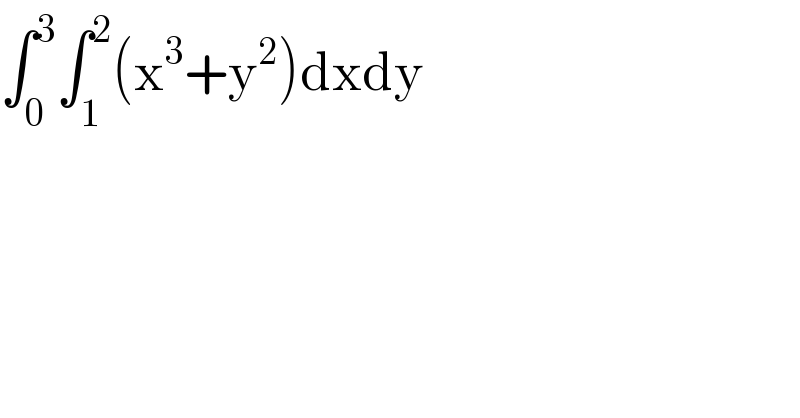
$$\int_{\mathrm{0}} ^{\mathrm{3}} \int_{\mathrm{1}} ^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{2}} \right)\mathrm{dxdy} \\ $$
Commented by Abdo msup. last updated on 20/Feb/19
![I =∫_0 ^3 A(y)dy with A(y)=∫_1 ^2 (x^3 +y^2 )dx =∫_1 ^2 x^3 dx +y^2 ∫_1 ^2 dx =[(x^4 /4)]_1 ^2 +y^2 =(1/4)( 2^4 −1) +y^2 =((15)/4) +y^2 ⇒ I =∫_0 ^3 (((15)/4)+y^2 )dy =((45)/4) +[(1/3)y^3 ]_0 ^3 =((45)/4) +9 =((45+36)/4) =((81)/4)](https://www.tinkutara.com/question/Q55242.png)
$${I}\:=\int_{\mathrm{0}} ^{\mathrm{3}} \:{A}\left({y}\right){dy}\:{with}\:{A}\left({y}\right)=\int_{\mathrm{1}} ^{\mathrm{2}} \left({x}^{\mathrm{3}} \:+{y}^{\mathrm{2}} \right){dx} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \:{x}^{\mathrm{3}} {dx}\:+{y}^{\mathrm{2}} \:\int_{\mathrm{1}} ^{\mathrm{2}} {dx}\:=\left[\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\right]_{\mathrm{1}} ^{\mathrm{2}} \:+{y}^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\:\mathrm{2}^{\mathrm{4}} −\mathrm{1}\right)\:+{y}^{\mathrm{2}} \:=\frac{\mathrm{15}}{\mathrm{4}}\:+{y}^{\mathrm{2}} \:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{3}} \:\left(\frac{\mathrm{15}}{\mathrm{4}}+{y}^{\mathrm{2}} \right){dy}\:=\frac{\mathrm{45}}{\mathrm{4}}\:+\left[\frac{\mathrm{1}}{\mathrm{3}}{y}^{\mathrm{3}} \right]_{\mathrm{0}} ^{\mathrm{3}} \\ $$$$=\frac{\mathrm{45}}{\mathrm{4}}\:+\mathrm{9}\:=\frac{\mathrm{45}+\mathrm{36}}{\mathrm{4}}\:=\frac{\mathrm{81}}{\mathrm{4}} \\ $$
Answered by kaivan.ahmadi last updated on 20/Feb/19
![∫_0 ^3 ((x^4 /4)+y^2 x]_1 ^2 )dy=∫_0 ^3 (4+2y^2 −(1/4)−y^2 )dy= ∫_0 ^3 (y^2 +((15)/4))dy=(y^3 /3)+((15)/4)y]_0 ^3 =9+((45)/4)=((81)/4)](https://www.tinkutara.com/question/Q55239.png)
$$\left.\int_{\mathrm{0}} ^{\mathrm{3}} \left(\frac{{x}^{\mathrm{4}} }{\mathrm{4}}+{y}^{\mathrm{2}} {x}\right]_{\mathrm{1}} ^{\mathrm{2}} \right){dy}=\int_{\mathrm{0}} ^{\mathrm{3}} \left(\mathrm{4}+\mathrm{2}{y}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}−{y}^{\mathrm{2}} \right){dy}= \\ $$$$\left.\int_{\mathrm{0}} ^{\mathrm{3}} \left({y}^{\mathrm{2}} +\frac{\mathrm{15}}{\mathrm{4}}\right){dy}=\frac{{y}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{15}}{\mathrm{4}}{y}\right]_{\mathrm{0}} ^{\mathrm{3}} =\mathrm{9}+\frac{\mathrm{45}}{\mathrm{4}}=\frac{\mathrm{81}}{\mathrm{4}} \\ $$$$ \\ $$
