Question Number 84087 by M±th+et£s last updated on 09/Mar/20
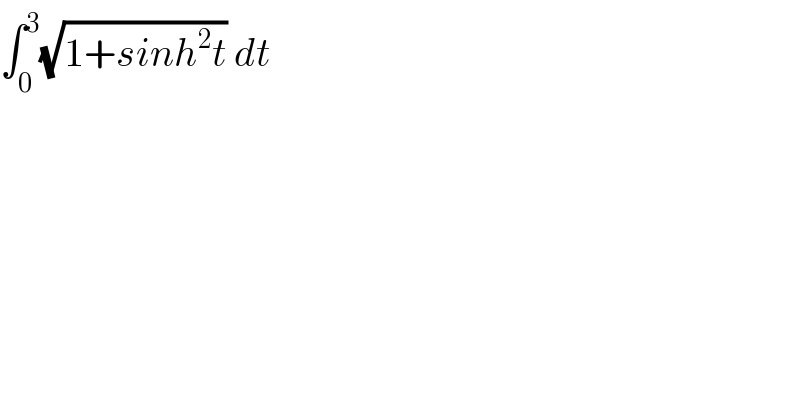
$$\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{\mathrm{1}+{sinh}^{\mathrm{2}} {t}}\:{dt} \\ $$
Commented by mathmax by abdo last updated on 09/Mar/20
![∫_0 ^3 (√(1+sh^2 t))dt =∫_0 ^3 ch(t)dt =[sh(t)]_0 ^3 =sh(3) =((e^3 −e^(−3) )/2)](https://www.tinkutara.com/question/Q84088.png)
$$\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{\mathrm{1}+{sh}^{\mathrm{2}} {t}}{dt}\:=\int_{\mathrm{0}} ^{\mathrm{3}} {ch}\left({t}\right){dt}\:=\left[{sh}\left({t}\right)\right]_{\mathrm{0}} ^{\mathrm{3}} ={sh}\left(\mathrm{3}\right)\:=\frac{{e}^{\mathrm{3}} −{e}^{−\mathrm{3}} }{\mathrm{2}} \\ $$
