Question Number 124217 by bramlexs22 last updated on 01/Dec/20
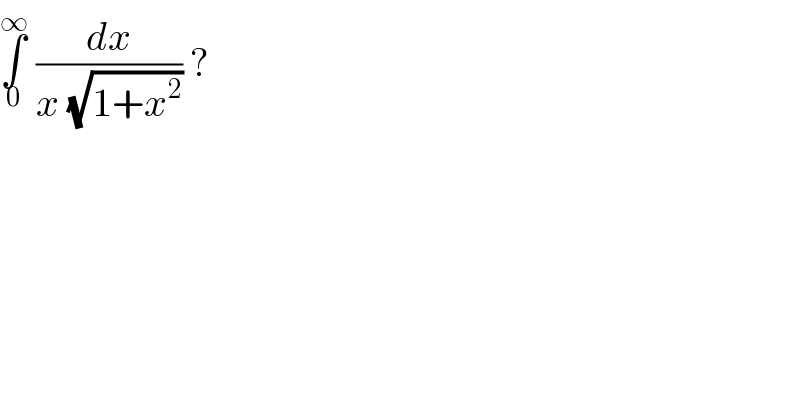
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{{dx}}{{x}\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 01/Dec/20
![(√(1+x^2 )) =t⇒(x/( (√(1+x^2 ))))=(dt/dx) =∫_1 ^∞ (1/x^2 )dt=∫_1 ^∞ (1/(t^2 −1))=[(1/2)log(((t−1)/(t+1)))]_1 ^∞ =doesn′t converge](https://www.tinkutara.com/question/Q124226.png)
$$\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:={t}\Rightarrow\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}=\frac{{dt}}{{dx}} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dt}=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{1}}=\left[\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\right)\right]_{\mathrm{1}} ^{\infty} ={doesn}'{t}\:{converge} \\ $$
