Question Number 98256 by M±th+et+s last updated on 12/Jun/20
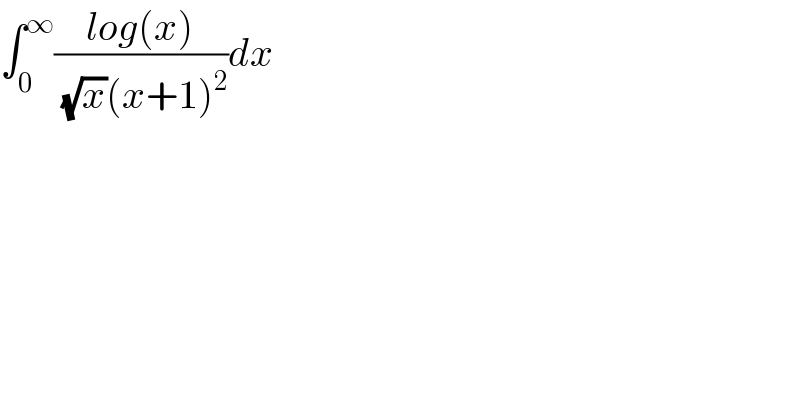
$$\int_{\mathrm{0}} ^{\infty} \frac{{log}\left({x}\right)}{\:\sqrt{{x}}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$
Answered by mathmax by abdo last updated on 12/Jun/20
![A =∫_0 ^∞ ((ln(x))/( (√x)(x+1)^2 ))dx changement (√x)=t give x=t^2 ⇒ A =∫_0 ^∞ ((ln(t^2 ))/(t(t^2 +1)^2 )) (2t)dt =4 ∫_0 ^∞ ((ln(t))/((1+t^2 )^2 ))dt A =4{ ∫_0 ^1 ((ln(t))/((1+t^2 )^2 ))dt +∫_1 ^(+∞) ((lnt)/((1+t^2 )^2 ))dt(→t=(1/u))} =4{ ∫_0 ^1 ((ln(t))/((1+t^2 )^2 ))dt −∫_0 ^1 ((−lnu)/((1+(1/u^2 ))^2 ))(−(du/u^2 ))} =4{ ∫_0 ^1 ((ln(t))/((1+t^2 )^2 ))dt−∫_0 ^1 ((ln(u)u^2 )/((1+u^2 )^2 ))} =4 ∫_0 ^1 (((1−t^2 )lnt)/((1+t^2 )^2 )) dt we have (1/(1+u)) =Σ_(n=0) ^∞ (−1)^n u^n ⇒−(1/((1+u)^2 )) =Σ_(n=1) ^∞ n(−1)^n u^(n−1) ⇒ (1/((1+u)^2 )) =−Σ_(n=1) ^∞ n(−1)^n u^(n−1) ⇒(1/((1+t^2 )^2 )) =−Σ_(n=1) ^∞ n(−1)^n t^(2n−2) ⇒ A =−4 ∫_0 ^1 (1−t^2 )ln(t)(Σ_(n=1) ^∞ n(−1)^n t^(2n−2) )dt =4 Σ_(n=1) ^∞ n(−1)^n ∫_0 ^1 (t^2 −1)t^(2n−2) ln(t)dt =4 Σ_(n=1) ^∞ n(−1)^n w_n W_n =∫_0 ^1 (t^(2n) −t^(2n−2) )ln(t)dt by parts W_n =[((t^(2n+1) /(2n+1)) −(t^(2n−1) /(2n−1)))ln(t)]_0 ^1 −∫_0 ^1 ((t^(2n+1) /(2n+1))−(t^(2n−1) /(2n−1)))(dt/t) =−(1/((2n+1)^2 )) +(1/((2n−1)^2 )) ⇒ A =4 Σ_(n=1) ^∞ n(−1)^n ((1/((2n−1)^2 ))−(1/((2n+1)^2 ))) =4 Σ_(n=1) ^∞ (−1)^n (n/((2n−1)^2 )) −4 Σ_(n=1) ^∞ (−1)^n (n/((2n+1)^2 )) Σ_(n=1) ^∞ ((n(−1)^n )/((2n−1)^2 )) =_(n=p+1) Σ_(p=0) ^∞ (((p+1)(−1)^(p+1) )/((2p+1)^2 )) =−1 −Σ_(n=1) ^∞ (((n+1)(−1)^n )/((2n+1)^2 )) =−1−Σ_(n=1) ^∞ ((n(−1)^n )/((2n+1)^2 )) −Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 )) ⇒ A =−4−4Σ_(n=1) ^∞ ((n(−1)^n )/((2n+1)^2 )) −4 Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 ))−4 Σ_(n=1) ^∞ ((n(−1)^n )/((2n+1)^2 )) =−4 −4 Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 )) −8 Σ_(n=1) ^∞ ((n(−1)^n )/((2n+1)^2 )) Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 )) =k−1 (k catalan constsnt) Σ_(n=1) ^∞ ((n(−1)^n )/((2n+1)^2 )) =(1/2)Σ_(n=1) ^∞ (((2n+1−1)(−1)^n )/((2n+1)^2 )) =(1/2) Σ_(n=1) ^∞ (((−1)^n )/((2n+1)))−(1/2)Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 )) =(1/2)((π/4)−1)−(1/2)(k−1) ⇒ A =−4 −4(k−1)−8{(π/8)−(1/2) −(1/2)(k−1)} =−4 −4(k−1)−π +4 +4(k−1) =−π ⇒ A =−π](https://www.tinkutara.com/question/Q98300.png)
$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{x}}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\mathrm{changement}\:\sqrt{\mathrm{x}}=\mathrm{t}\:\mathrm{give}\:\mathrm{x}=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\left(\mathrm{2t}\right)\mathrm{dt}\:=\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}\:\: \\ $$$$\mathrm{A}\:=\mathrm{4}\left\{\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}\:+\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{lnt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}\left(\rightarrow\mathrm{t}=\frac{\mathrm{1}}{\mathrm{u}}\right)\right\} \\ $$$$=\mathrm{4}\left\{\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{−\mathrm{lnu}}{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }\right)^{\mathrm{2}} }\left(−\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} }\right)\right\} \\ $$$$=\mathrm{4}\left\{\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{u}\right)\mathrm{u}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{2}} }\right\}\:=\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)\mathrm{lnt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\mathrm{dt} \\ $$$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{n}} \:\Rightarrow−\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} }\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{n}−\mathrm{1}} \:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} }\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{n}−\mathrm{1}} \:\Rightarrow\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{t}^{\mathrm{2n}−\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{A}\:=−\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)\mathrm{ln}\left(\mathrm{t}\right)\left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{t}^{\mathrm{2n}−\mathrm{2}} \right)\mathrm{dt} \\ $$$$=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{t}^{\mathrm{2n}−\mathrm{2}} \:\mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt}\:=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{w}_{\mathrm{n}} \\ $$$$\mathrm{W}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\mathrm{t}^{\mathrm{2n}} \:−\mathrm{t}^{\mathrm{2n}−\mathrm{2}} \right)\mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt}\:\:\mathrm{by}\:\mathrm{parts}\: \\ $$$$\mathrm{W}_{\mathrm{n}} =\left[\left(\frac{\mathrm{t}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\:−\frac{\mathrm{t}^{\mathrm{2n}−\mathrm{1}} }{\mathrm{2n}−\mathrm{1}}\right)\mathrm{ln}\left(\mathrm{t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{t}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}−\frac{\mathrm{t}^{\mathrm{2n}−\mathrm{1}} }{\mathrm{2n}−\mathrm{1}}\right)\frac{\mathrm{dt}}{\mathrm{t}} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\left(\mathrm{2n}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\:\mathrm{A}\:=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\frac{\mathrm{1}}{\left(\mathrm{2n}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\frac{\mathrm{n}}{\left(\mathrm{2n}−\mathrm{1}\right)^{\mathrm{2}} }\:−\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\frac{\mathrm{n}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}−\mathrm{1}\right)^{\mathrm{2}} }\:=_{\mathrm{n}=\mathrm{p}+\mathrm{1}} \:\:\:\:\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{p}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{p}+\mathrm{1}} }{\left(\mathrm{2p}+\mathrm{1}\right)^{\mathrm{2}} }\:=−\mathrm{1}\:−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=−\mathrm{1}−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{A}\:=−\mathrm{4}−\mathrm{4}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:−\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=−\mathrm{4}\:−\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:−\mathrm{8}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{k}−\mathrm{1}\:\:\:\left(\mathrm{k}\:\mathrm{catalan}\:\mathrm{constsnt}\right) \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(\mathrm{2n}+\mathrm{1}−\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{4}}−\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{k}−\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{A}\:=−\mathrm{4}\:−\mathrm{4}\left(\mathrm{k}−\mathrm{1}\right)−\mathrm{8}\left\{\frac{\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{k}−\mathrm{1}\right)\right\} \\ $$$$=−\mathrm{4}\:−\mathrm{4}\left(\mathrm{k}−\mathrm{1}\right)−\pi\:\:+\mathrm{4}\:+\mathrm{4}\left(\mathrm{k}−\mathrm{1}\right)\:=−\pi\:\Rightarrow\:\mathrm{A}\:=−\pi \\ $$
Commented by M±th+et+s last updated on 12/Jun/20

$${well}\:{done}\:.\: \\ $$$${correct}\:{solution} \\ $$
Answered by maths mind last updated on 13/Jun/20
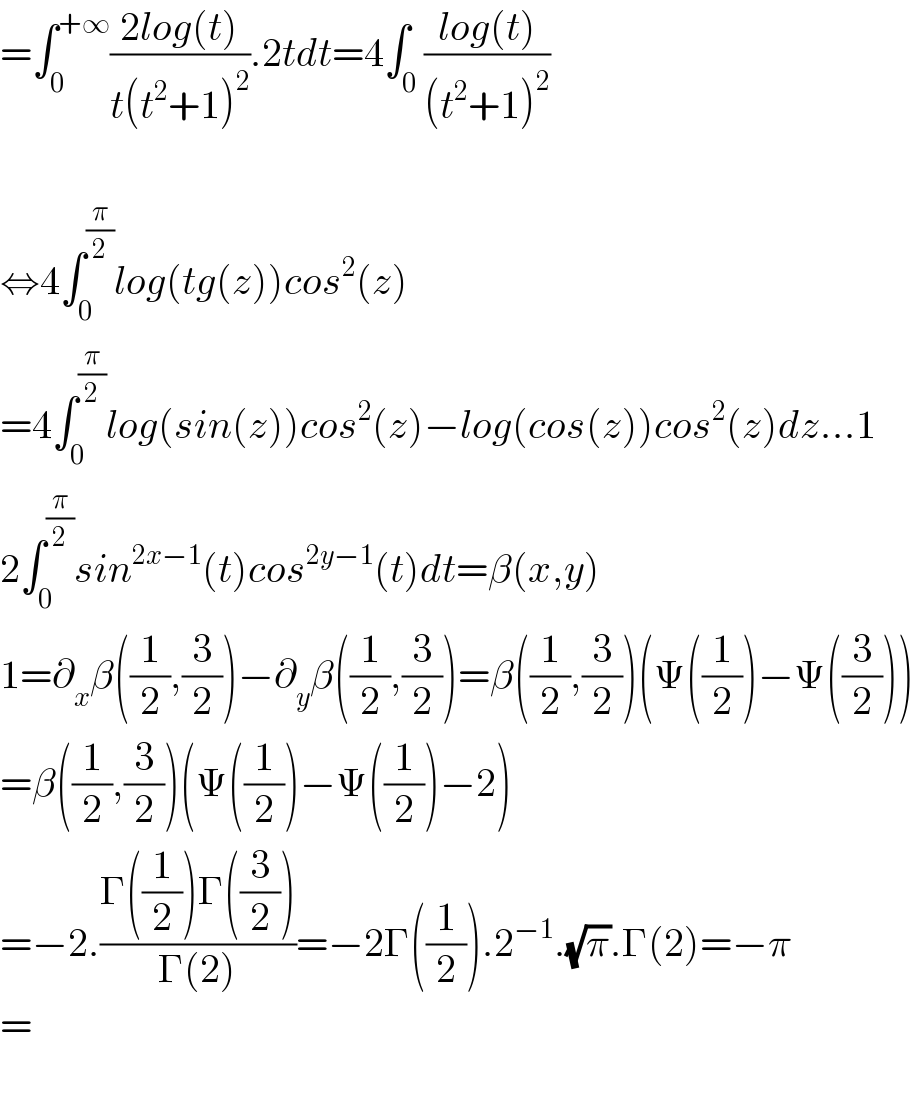
$$=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{2}{log}\left({t}\right)}{{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }.\mathrm{2}{tdt}=\mathrm{4}\int_{\mathrm{0}} \frac{{log}\left({t}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$\Leftrightarrow\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({tg}\left({z}\right)\right){cos}^{\mathrm{2}} \left({z}\right) \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sin}\left({z}\right)\right){cos}^{\mathrm{2}} \left({z}\right)−{log}\left({cos}\left({z}\right)\right){cos}^{\mathrm{2}} \left({z}\right){dz}…\mathrm{1} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}{x}−\mathrm{1}} \left({t}\right){cos}^{\mathrm{2}{y}−\mathrm{1}} \left({t}\right){dt}=\beta\left({x},{y}\right) \\ $$$$\mathrm{1}=\partial_{{x}} \beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right)−\partial_{{y}} \beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right)=\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right)\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right) \\ $$$$=\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right)\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}\right) \\ $$$$=−\mathrm{2}.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}\right)}=−\mathrm{2}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right).\mathrm{2}^{−\mathrm{1}} .\sqrt{\pi}.\Gamma\left(\mathrm{2}\right)=−\pi \\ $$$$= \\ $$$$ \\ $$
Commented by maths mind last updated on 13/Jun/20
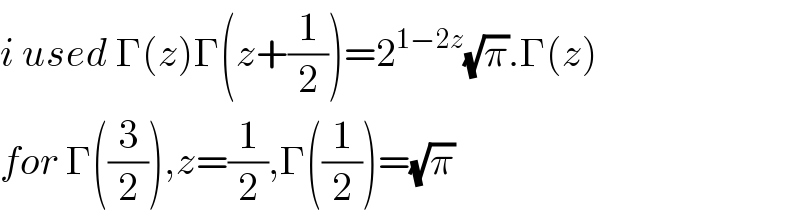
$${i}\:{used}\:\Gamma\left({z}\right)\Gamma\left({z}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}^{\mathrm{1}−\mathrm{2}{z}} \sqrt{\pi}.\Gamma\left({z}\right) \\ $$$${for}\:\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right),{z}=\frac{\mathrm{1}}{\mathrm{2}},\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\pi} \\ $$
Commented by M±th+et+s last updated on 13/Jun/20

$${very}\:{nice}\:{sir}\:{thanx} \\ $$
