Question Number 21721 by Isse last updated on 02/Oct/17
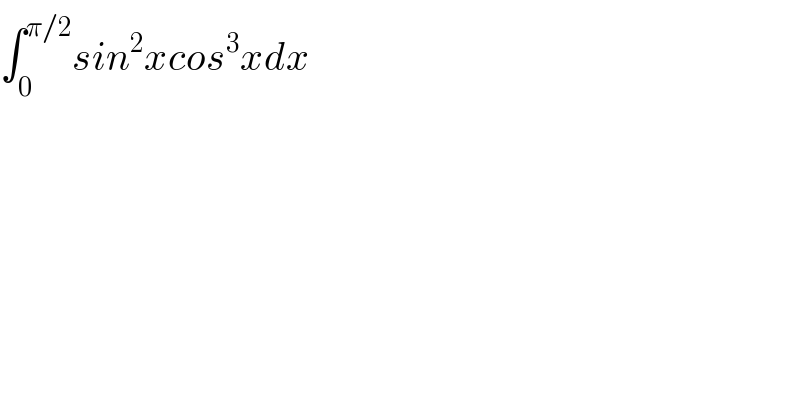
$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {sin}^{\mathrm{2}} {xcos}^{\mathrm{3}} {xdx} \\ $$
Answered by sma3l2996 last updated on 02/Oct/17
![=∫_0 ^(π/2) sin^2 x(1−sin^2 x)cosxdx=∫_0 ^(π/2) (cosxsin^2 x−cosxsin^4 x)dx =[(1/3)sin^3 x−(1/5)sin^5 x]_0 ^(π/2) =(1/3)−(1/5)=(2/(15))](https://www.tinkutara.com/question/Q21724.png)
$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {sin}^{\mathrm{2}} {x}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right){cosxdx}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({cosxsin}^{\mathrm{2}} {x}−{cosxsin}^{\mathrm{4}} {x}\right){dx} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{3}}{sin}^{\mathrm{3}} {x}−\frac{\mathrm{1}}{\mathrm{5}}{sin}^{\mathrm{5}} {x}\right]_{\mathrm{0}} ^{\pi/\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}=\frac{\mathrm{2}}{\mathrm{15}} \\ $$
