Question Number 129490 by 676597498 last updated on 16/Jan/21
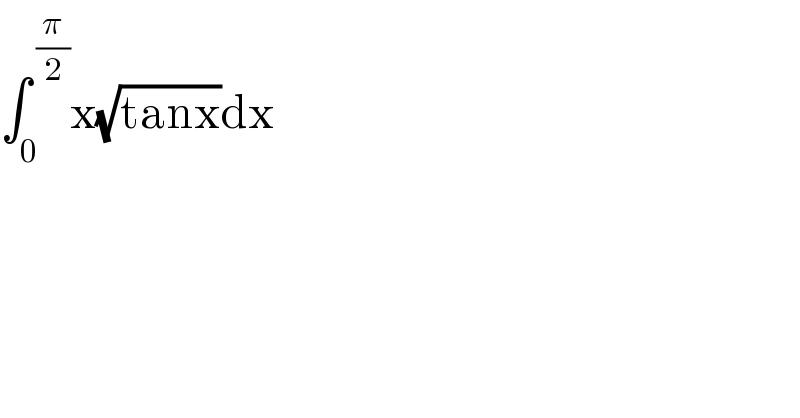
$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{x}\sqrt{\mathrm{tanx}}\mathrm{dx} \\ $$
Answered by mnjuly1970 last updated on 16/Jan/21
![Ω=∫_0 ^( (π/2)) x.sin^(1/2) (x).cos^(1/2) (x)dx =(π/2)∫_0 ^( (π/2)) sin^(1/2) (x).cos^(1/2) (x)−Ω 2Ω=(π/4)[2∫_0 ^( (π/2)) sin^(1/2) (x).cos^(1/2) (x)dx] =(π/4) (β((3/4) , (3/4)))=(π/4)∗((Γ^2 ((3/4)))/(Γ((3/2)))) ∴ Ω=(π/8)∗((Γ^2 ((3/4)))/((1/2)Γ((1/2))))=(π/(4(√π) ))∗Γ^2 ((3/4))](https://www.tinkutara.com/question/Q129500.png)
$$\:\Omega=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {x}.{sin}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({x}\right).{cos}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({x}\right){dx}\: \\ $$$$\:\:\:\:=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {sin}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({x}\right).{cos}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({x}\right)−\Omega \\ $$$$\mathrm{2}\Omega=\frac{\pi}{\mathrm{4}}\left[\mathrm{2}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {sin}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({x}\right).{cos}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({x}\right){dx}\right] \\ $$$$\:\:\:\:\:\:=\frac{\pi}{\mathrm{4}}\:\left(\beta\left(\frac{\mathrm{3}}{\mathrm{4}}\:,\:\frac{\mathrm{3}}{\mathrm{4}}\right)\right)=\frac{\pi}{\mathrm{4}}\ast\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)}{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$\:\:\:\therefore\:\:\Omega=\frac{\pi}{\mathrm{8}}\ast\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)}{\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\pi}{\mathrm{4}\sqrt{\pi}\:}\ast\Gamma\:^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$
