Question Number 116311 by bemath last updated on 03/Oct/20
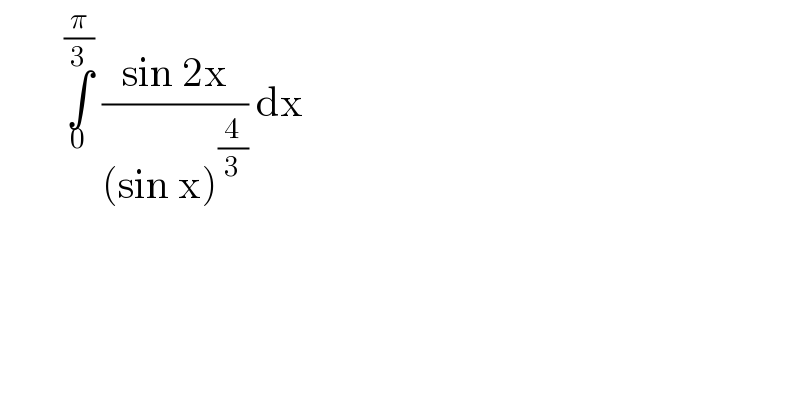
$$\:\:\:\:\:\:\:\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{3}}} {\int}}\:\frac{\mathrm{sin}\:\mathrm{2x}}{\left(\mathrm{sin}\:\mathrm{x}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} }\:\mathrm{dx}\: \\ $$$$ \\ $$
Answered by bobhans last updated on 03/Oct/20
![let sin x = u with { ((u=((√3)/2))),((u=0)) :} I = ∫_0 ^((√3)/2) ((2u du)/u^(4/3) ) = 2∫_0 ^((√3)/2) u^(−(1/3)) du I= 2[ (3/2)u^(2/3) ]_0 ^((√3)/2) = 3(((√3)/2))^(2/3) =3((3/4))^(1/(3 )) = 3 ((6/8))^(1/(3 )) = ((3 (6)^(1/(3 )) )/2) .](https://www.tinkutara.com/question/Q116312.png)
$$\mathrm{let}\:\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{u}\:\mathrm{with}\:\begin{cases}{\mathrm{u}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\\{\mathrm{u}=\mathrm{0}}\end{cases} \\ $$$$\mathrm{I}\:=\:\underset{\mathrm{0}} {\overset{\sqrt{\mathrm{3}}/\mathrm{2}} {\int}}\:\frac{\mathrm{2u}\:\mathrm{du}}{\mathrm{u}^{\frac{\mathrm{4}}{\mathrm{3}}} }\:=\:\mathrm{2}\underset{\mathrm{0}} {\overset{\sqrt{\mathrm{3}}/\mathrm{2}} {\int}}\mathrm{u}^{−\frac{\mathrm{1}}{\mathrm{3}}} \:\mathrm{du} \\ $$$$\mathrm{I}=\:\mathrm{2}\left[\:\frac{\mathrm{3}}{\mathrm{2}}\mathrm{u}^{\frac{\mathrm{2}}{\mathrm{3}}} \:\right]_{\mathrm{0}} ^{\sqrt{\mathrm{3}}/\mathrm{2}} =\:\mathrm{3}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} =\mathrm{3}\sqrt[{\mathrm{3}\:}]{\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=\:\mathrm{3}\:\sqrt[{\mathrm{3}\:}]{\frac{\mathrm{6}}{\mathrm{8}}}\:=\:\frac{\mathrm{3}\:\sqrt[{\mathrm{3}\:}]{\mathrm{6}}}{\mathrm{2}}\:. \\ $$
Answered by Bird last updated on 03/Oct/20
![I =∫_0 ^(π/3) ((2sinx cosx)/((sinx)^(4/3) ))dx =_(sinx=t) 2∫_0 ^((√3)/2) ((t(√(1−t^2 )))/t^(4/3) )(dt/( (√(1−t^2 )))) =2 ∫_0 ^((√3)/2) t^(1−(4/3)) dt =2 ∫_0 ^((√3)/2) t^(−(1/3)) dt =2[(1/(1−(1/3)))t^(1−(1/3)) ]_0 ^((√3)/2) =2[(3/2)t^(2/3) ]_0 ^((√3)/2) =3((((√3)/2))^(2/3) ) =3(^3 (√(3/4)))](https://www.tinkutara.com/question/Q116313.png)
$${I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{\mathrm{2}{sinx}\:{cosx}}{\left({sinx}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} }{dx} \\ $$$$=_{{sinx}={t}} \:\:\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \:\:\frac{{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{{t}^{\frac{\mathrm{4}}{\mathrm{3}}} }\frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \:\:{t}^{\mathrm{1}−\frac{\mathrm{4}}{\mathrm{3}}} \:{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \:{t}^{−\frac{\mathrm{1}}{\mathrm{3}}} {dt} \\ $$$$=\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}{t}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}} \right]_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \\ $$$$=\mathrm{2}\left[\frac{\mathrm{3}}{\mathrm{2}}{t}^{\frac{\mathrm{2}}{\mathrm{3}}} \right]_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} =\mathrm{3}\left(\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \right) \\ $$$$=\mathrm{3}\left(^{\mathrm{3}} \sqrt{\frac{\mathrm{3}}{\mathrm{4}}}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 03/Oct/20
![∫_0 ^(π/3) ((sin2x)/((sinx)^(4/3) ))dx ∫_0 ^(π/3) ((2cosx)/(sin^(1/3) x))dx =2∫_0 ^((√3)/2) (dt/t^(1/3) )=3[t^(2/3) ]^((√3)/2) =3(((√3)/2))^(2/3) =3^(4/3) ((1/2))^(2/3)](https://www.tinkutara.com/question/Q116337.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \frac{\mathrm{sin2x}}{\left(\mathrm{sinx}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} }\mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \frac{\mathrm{2cosx}}{\mathrm{sin}^{\frac{\mathrm{1}}{\mathrm{3}}} \mathrm{x}}\mathrm{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \frac{\mathrm{dt}}{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}} }=\mathrm{3}\left[\mathrm{t}^{\frac{\mathrm{2}}{\mathrm{3}}} \right]^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} =\mathrm{3}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} =\mathrm{3}^{\frac{\mathrm{4}}{\mathrm{3}}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$
