Question Number 122979 by bemath last updated on 21/Nov/20
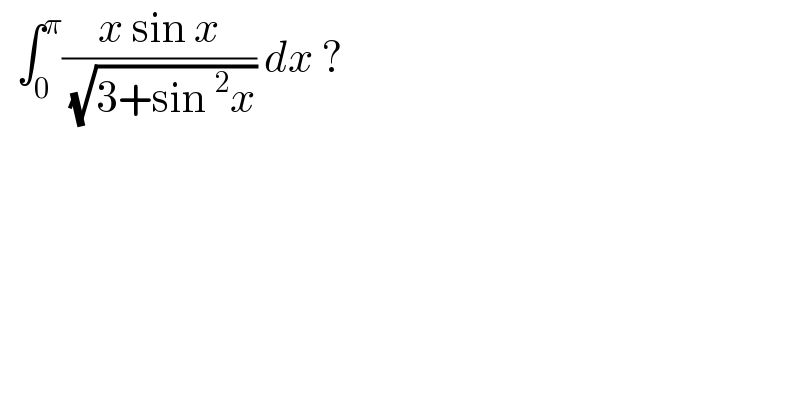
$$\:\:\int_{\mathrm{0}} ^{\pi} \frac{{x}\:\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{3}+\mathrm{sin}\:^{\mathrm{2}} {x}}}\:{dx}\:? \\ $$
Answered by liberty last updated on 21/Nov/20
![ψ(x)=∫_0 ^π ((xsin x)/( (√(4−cos^2 x)))) dx replacing x by π−x , give ψ(x)=∫_π ^0 (((π−x)sin (π−x))/( (√(4−cos^2 (π−x))))) (−dx) ψ(x)=∫_0 ^π (((π−x)sin x)/( (√(4−cos^2 x)))) dx adding the both integral , we obtain 2ψ(x)=∫_0 ^π ((πsin x)/( (√((2)^2 −cos^2 (x))))) dx ψ(x)=−(π/2)[sin^(−1) (((cos x)/2))]_0 ^π ψ(x)=−(π/2)(−(π/3))=(π/6). ▲](https://www.tinkutara.com/question/Q122984.png)
$$\psi\left({x}\right)=\int_{\mathrm{0}} ^{\pi} \frac{{x}\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{4}−\mathrm{cos}\:^{\mathrm{2}} {x}}}\:{dx} \\ $$$$\:{replacing}\:{x}\:{by}\:\pi−{x}\:,\:{give}\: \\ $$$$\psi\left({x}\right)=\int_{\pi} ^{\mathrm{0}} \frac{\left(\pi−{x}\right)\mathrm{sin}\:\left(\pi−{x}\right)}{\:\sqrt{\mathrm{4}−\mathrm{cos}\:^{\mathrm{2}} \left(\pi−{x}\right)}}\:\left(−{dx}\right) \\ $$$$\psi\left({x}\right)=\int_{\mathrm{0}} ^{\pi} \frac{\left(\pi−{x}\right)\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{4}−\mathrm{cos}\:^{\mathrm{2}} {x}}}\:{dx}\: \\ $$$${adding}\:{the}\:{both}\:{integral}\:,\:{we}\:{obtain} \\ $$$$\mathrm{2}\psi\left({x}\right)=\int_{\mathrm{0}} ^{\pi} \frac{\pi\mathrm{sin}\:{x}}{\:\sqrt{\left(\mathrm{2}\right)^{\mathrm{2}} −\mathrm{cos}\:^{\mathrm{2}} \left({x}\right)}}\:{dx} \\ $$$$\psi\left({x}\right)=−\frac{\pi}{\mathrm{2}}\left[\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:{x}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\pi} \\ $$$$\psi\left({x}\right)=−\frac{\pi}{\mathrm{2}}\left(−\frac{\pi}{\mathrm{3}}\right)=\frac{\pi}{\mathrm{6}}.\:\blacktriangle \\ $$$$ \\ $$
