Question Number 99413 by maths mind last updated on 20/Jun/20
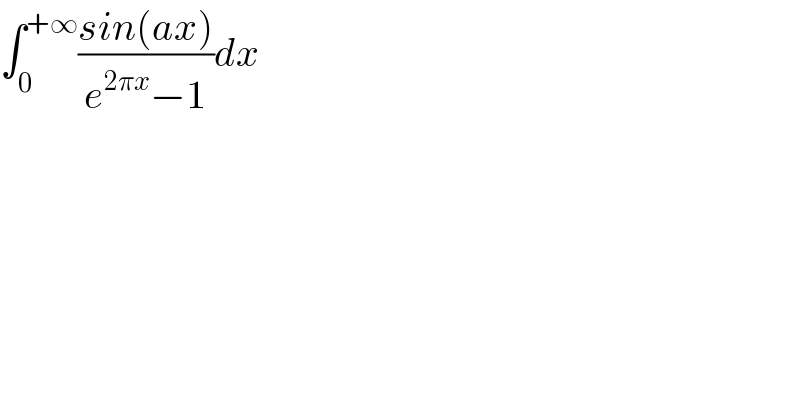
$$\int_{\mathrm{0}} ^{+\infty} \frac{{sin}\left({ax}\right)}{{e}^{\mathrm{2}\pi{x}} −\mathrm{1}}{dx} \\ $$
Answered by mathmax by abdo last updated on 20/Jun/20
![I =∫_0 ^∞ ((sin(ax))/(e^(2πx) −1))dx ⇒I = ∫_0 ^∞ ((e^(−2πx) sin(ax))/(1−e^(−2πx) )) =∫_0 ^∞ e^(−2πx) sin(ax)Σ_(n=0) ^∞ e^(−2πnx) dx =Σ_(n=0) ^∞ ∫_0 ^∞ e^(−(2π+2πn)x) sin(ax) dx =_(2π(n+1)x =t) Σ_(n=0) ^∞ ∫_0 ^∞ e^(−t) sin(a(t/(2π(n+1))))(dt/(2π(n+1))) =(1/(2π)) Σ_(n=0) ^∞ (1/(n+1)) ∫_0 ^∞ e^(−t) sin(((at)/(2π(n+1))))dt we have ∫_0 ^∞ e^(−t) sin(((at)/(2π(n+1))))dt =Im(∫_0 ^∞ e^(−(1+((ai)/(2π(n+1))))t) dt) and ∫_0 ^∞ e^(−(1+((ai)/(2π(n+1))))t) dt =[−(1/(1+((ai)/(2π(n+1))))) e^(−(1+((ai)/(2π(n+1))))t) ]_0 ^∞ =(1/(1+((ai)/(2π(n+1))))) =((2π(n+1))/(2π(n+1)+ai)) =((2π(n+1)(2π(n+1)−ai))/(4π^2 (n+1)^2 +a^2 )) ⇒ Im(∫_0 ^∞ (....)dt) =((−2πa(n+1))/(4π^2 (n+1)^2 +a^2 )) ⇒ I =(1/(2π))Σ_(n=0) ^∞ (1/((n+1)))×((−2πa(n+1))/(4π^2 (n+1)^2 +a^2 )) =−a Σ_(n=0) ^∞ (1/(4π^2 (n+1)^2 +a^2 )) and this serie can be found by fourier ....](https://www.tinkutara.com/question/Q99427.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{ax}\right)}{\mathrm{e}^{\mathrm{2}\pi\mathrm{x}} −\mathrm{1}}\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{−\mathrm{2}\pi\mathrm{x}} \:\mathrm{sin}\left(\mathrm{ax}\right)}{\mathrm{1}−\mathrm{e}^{−\mathrm{2}\pi\mathrm{x}} }\:=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{2}\pi\mathrm{x}} \mathrm{sin}\left(\mathrm{ax}\right)\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{2}\pi\mathrm{nx}} \:\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{2}\pi+\mathrm{2}\pi\mathrm{n}\right)\mathrm{x}} \:\mathrm{sin}\left(\mathrm{ax}\right)\:\mathrm{dx}\:\:=_{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}\:=\mathrm{t}} \:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{sin}\left(\mathrm{a}\frac{\mathrm{t}}{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)}\right)\frac{\mathrm{dt}}{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{sin}\left(\frac{\mathrm{at}}{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)}\right)\mathrm{dt}\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{sin}\left(\frac{\mathrm{at}}{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)}\right)\mathrm{dt}\:=\mathrm{Im}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{1}+\frac{\mathrm{ai}}{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)}\right)\mathrm{t}} \:\mathrm{dt}\right)\:\mathrm{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{1}+\frac{\mathrm{ai}}{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)}\right)\mathrm{t}} \:\mathrm{dt}\:=\left[−\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{ai}}{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)}}\:\mathrm{e}^{−\left(\mathrm{1}+\frac{\mathrm{ai}}{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{ai}}{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)}}\:=\frac{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{ai}}\:=\frac{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)−\mathrm{ai}\right)}{\mathrm{4}\pi^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{Im}\left(\int_{\mathrm{0}} ^{\infty} \:\left(….\right)\mathrm{dt}\right)\:=\frac{−\mathrm{2}\pi\mathrm{a}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{4}\pi^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{2}\pi}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)}×\frac{−\mathrm{2}\pi\mathrm{a}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{4}\pi^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\:=−\mathrm{a}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{4}\pi^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{and}\:\mathrm{this}\:\mathrm{serie}\:\mathrm{can}\:\mathrm{be}\:\mathrm{found}\:\mathrm{by}\:\mathrm{fourier}\:…. \\ $$
Commented by maths mind last updated on 20/Jun/20

$${nice}\:{sir}\:\:{thank}\:{you}\:{for}\:{the}\:{solution}\:{and}\:{your}\:{time} \\ $$
Commented by abdomathmax last updated on 20/Jun/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$
