Question Number 125911 by Lordose last updated on 15/Dec/20
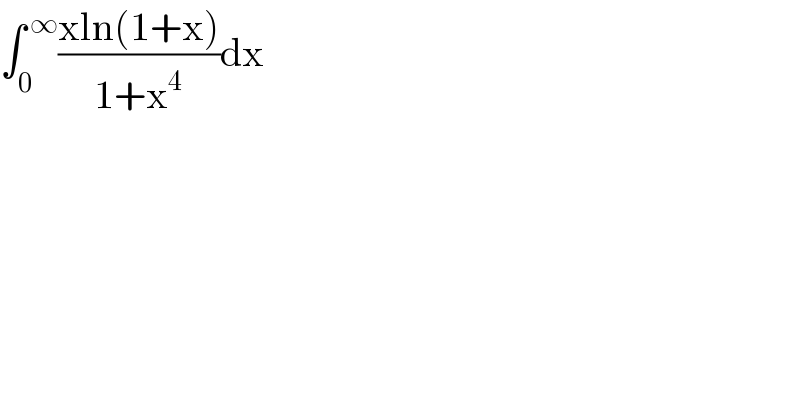
$$\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{xln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 15/Dec/20
![A =∫_0 ^∞ ((xln(1+x))/(1+x^4 ))dx =∫_0 ^1 ((xln(1+x))/(1+x^4 ))dx+∫_1 ^∞ ((xln(x+1))/(1+x^4 ))dx ∫_1 ^∞ ((xln(x+1))/(1+x^4 ))dx =_(x=(1/t)) −∫_0 ^1 ((ln(1+(1/t)))/(t(1+(1/t^4 ))))(−(dt/t^2 )) =∫_0 ^1 ((ln(t+1)−ln(t)/(t^3 +(1/t)))dt =∫_0 ^1 ((tln(t+1)−tlnt)/(1+t^4 ))dt ⇒A =2∫_0 ^1 ((xln(x+1))/(1+x^4 ))dx−∫_0 ^1 ((xlnx)/(1+x^4 ))dx we have ∫_0 ^1 ((xlnx)/(1+x^4 ))dx =∫_0 ^1 xln(x)Σ_(n=0) ^∞ (−1)^n x^(4n) dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(4n+1) ln(x)dx =Σ_(n=0) ^∞ (−1)^n u_n u_n =∫_0 ^1 x^(4n+1) ln(x)dx =[(1/(4n+2))x^(4n+2) ln(x)]_0 ^1 −∫_0 ^1 (x^(4n+1) /(4n+2))dx =−(1/((4n+2)^2 )) ⇒∫_0 ^1 ((xlnx)/(1+x^4 ))dx =−Σ_(n=0) ^∞ (((−1)^n )/(4(2n+1)^2 )) =−(k/4)( katalan constant) ∫_0 ^1 ((xln(x+1))/(1+x^4 ))dx =∫_0 ^1 xln(x+1)Σ_(n=0) ^∞ (−1)^n x^(4n) dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(4n+1) ln(x+1)dx =Σ_(n=0) ^∞ (−1)^n v_n v_n =∫_0 ^1 x^(4n+1) ln(x+1)dx =_(x+1=t) ∫_1 ^2 (t−1)^(4n+1) ln(t)dt =∫_1 ^2 ln(t)Σ_(k=0) ^(4n+1) C_(4n+1) ^k t^k (−1)^(4n+1−k) dt =−Σ_(k=0) ^(4n+1) (−1)^k C_(4n+1) ^k ∫_1 ^2 t^(k ) ln(t)dt and by psrts ∫_1 ^2 t^k ln(t)dt =[(1/(k+1))t^(k+1) ln(t)]_1 ^2 −∫_1 ^2 (t^(k+1) /(k+1))(dt/t) =((2^(k+1) ln(2))/(k+1))−(1/(k+1))∫_1 ^2 t^k dt =((2^(k+1) ln(2))/(k+1))−(1/((k+1)^2 ))[t^(k+1) ]_1 ^2 =((2^(k+1) ln(2))/(k+1))−(1/((k+1)^2 ))(2^(k+1) −1) ⇒ v_n =−Σ_(k=0) ^(4n+1) (−1)^k C_(4n+1) ^k {((2^(k+1) ln(2))/(k+1))−((2^(k+1) −1)/((k+1)^2 ))} ....be continued...](https://www.tinkutara.com/question/Q125956.png)
$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{xln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{xln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}+\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{xln}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx} \\ $$$$\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{xln}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:=_{\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}} \:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}}\right)}{\mathrm{t}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{4}} }\right)}\left(−\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{t}+\mathrm{1}\right)−\mathrm{ln}\left(\mathrm{t}\right.}{\mathrm{t}^{\mathrm{3}} \:+\frac{\mathrm{1}}{\mathrm{t}}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{tln}\left(\mathrm{t}+\mathrm{1}\right)−\mathrm{tlnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }\mathrm{dt} \\ $$$$\Rightarrow\mathrm{A}\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{xln}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{xlnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{xlnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{xln}\left(\mathrm{x}\right)\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{4n}} \mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{4n}+\mathrm{1}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}_{\mathrm{n}} \\ $$$$\mathrm{u}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{4n}+\mathrm{1}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx}\:=\left[\frac{\mathrm{1}}{\mathrm{4n}+\mathrm{2}}\mathrm{x}^{\mathrm{4n}+\mathrm{2}} \mathrm{ln}\left(\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{4n}+\mathrm{1}} }{\mathrm{4n}+\mathrm{2}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{4n}+\mathrm{2}\right)^{\mathrm{2}} }\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{xlnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{4}\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{k}}{\mathrm{4}}\left(\:\mathrm{katalan}\:\mathrm{constant}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{xln}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{xln}\left(\mathrm{x}+\mathrm{1}\right)\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{4n}} \:\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{4n}+\mathrm{1}} \:\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{v}_{\mathrm{n}} \\ $$$$\mathrm{v}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{4n}+\mathrm{1}} \mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)\mathrm{dx}\:=_{\mathrm{x}+\mathrm{1}=\mathrm{t}} \:\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{4n}+\mathrm{1}} \mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \:\mathrm{ln}\left(\mathrm{t}\right)\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4n}+\mathrm{1}} \:\mathrm{C}_{\mathrm{4n}+\mathrm{1}} ^{\mathrm{k}} \:\mathrm{t}^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{4n}+\mathrm{1}−\mathrm{k}} \:\mathrm{dt} \\ $$$$=−\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4n}+\mathrm{1}} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{4n}+\mathrm{1}} ^{\mathrm{k}} \:\int_{\mathrm{1}} ^{\mathrm{2}} \:\mathrm{t}^{\mathrm{k}\:} \mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt}\:\:\:\mathrm{and}\:\mathrm{by}\:\mathrm{psrts} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \:\mathrm{t}^{\mathrm{k}} \:\mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt}\:=\left[\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\mathrm{t}^{\mathrm{k}+\mathrm{1}} \mathrm{ln}\left(\mathrm{t}\right)\right]_{\mathrm{1}} ^{\mathrm{2}} −\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{\mathrm{t}^{\mathrm{k}+\mathrm{1}} }{\mathrm{k}+\mathrm{1}}\frac{\mathrm{dt}}{\mathrm{t}} \\ $$$$=\frac{\mathrm{2}^{\mathrm{k}+\mathrm{1}} \mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{k}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\mathrm{t}^{\mathrm{k}} \:\mathrm{dt}\:=\frac{\mathrm{2}^{\mathrm{k}+\mathrm{1}} \mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{k}+\mathrm{1}}−\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }\left[\mathrm{t}^{\mathrm{k}+\mathrm{1}} \right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$=\frac{\mathrm{2}^{\mathrm{k}+\mathrm{1}} \mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{k}+\mathrm{1}}−\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }\left(\mathrm{2}^{\mathrm{k}+\mathrm{1}} −\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{v}_{\mathrm{n}} =−\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4n}+\mathrm{1}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{4n}+\mathrm{1}} ^{\mathrm{k}} \left\{\frac{\mathrm{2}^{\mathrm{k}+\mathrm{1}} \mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{k}+\mathrm{1}}−\frac{\mathrm{2}^{\mathrm{k}+\mathrm{1}} −\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }\right\} \\ $$$$….\mathrm{be}\:\mathrm{continued}… \\ $$$$ \\ $$
