Question Number 109495 by qwerty111 last updated on 24/Aug/20
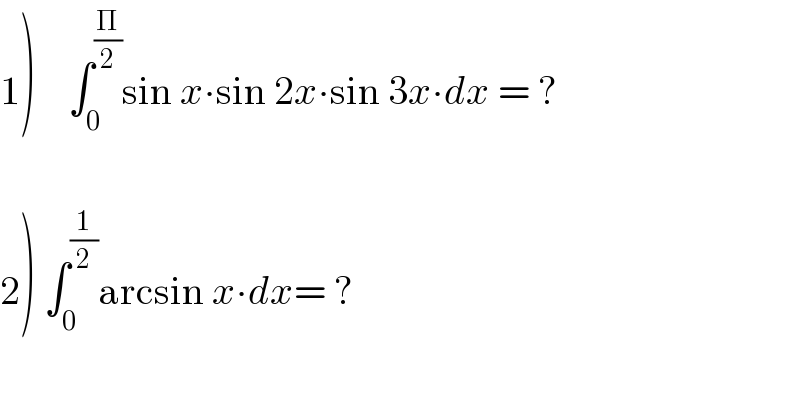
$$\left.\mathrm{1}\right)\:\:\:\:\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \mathrm{sin}\:{x}\centerdot\mathrm{sin}\:\mathrm{2}{x}\centerdot\mathrm{sin}\:\mathrm{3}{x}\centerdot{dx}\:=\:? \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{arcsin}\:{x}\centerdot{dx}=\:? \\ $$
Answered by bemath last updated on 24/Aug/20
![1) sin 3x = 3sin x−4sin^3 x I=∫_0 ^(π/2) 2sin^2 x.(3sin x−4sin^3 x)cos x dx= set u = sin x → { ((u=1)),((u=0)) :} I=∫_0 ^1 2u^2 (3u−4u^3 ) du = I= ∫_0 ^1 (6u^3 −8u^5 )du = [(3/2)u^4 −(4/3)u^6 ]_0 ^1 = (3/2)−(4/3) = (1/6)](https://www.tinkutara.com/question/Q109496.png)
$$\left.\mathrm{1}\right)\:\mathrm{sin}\:\mathrm{3}{x}\:=\:\mathrm{3sin}\:{x}−\mathrm{4sin}\:^{\mathrm{3}} {x} \\ $$$${I}=\overset{\pi/\mathrm{2}} {\int}_{\mathrm{0}} \mathrm{2sin}^{\mathrm{2}} \:{x}.\left(\mathrm{3sin}\:{x}−\mathrm{4sin}\:^{\mathrm{3}} {x}\right)\mathrm{cos}\:{x}\:{dx}= \\ $$$${set}\:{u}\:=\:\mathrm{sin}\:{x}\:\rightarrow\begin{cases}{{u}=\mathrm{1}}\\{{u}=\mathrm{0}}\end{cases} \\ $$$${I}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\mathrm{2}{u}^{\mathrm{2}} \:\left(\mathrm{3}{u}−\mathrm{4}{u}^{\mathrm{3}} \right)\:{du}\:= \\ $$$${I}=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\mathrm{6}{u}^{\mathrm{3}} −\mathrm{8}{u}^{\mathrm{5}} \right){du}\:=\:\left[\frac{\mathrm{3}}{\mathrm{2}}{u}^{\mathrm{4}} −\frac{\mathrm{4}}{\mathrm{3}}{u}^{\mathrm{6}} \:\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\:\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{4}}{\mathrm{3}}\:=\:\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$ \\ $$
Answered by bemath last updated on 24/Aug/20
![(2) by part { ((u=arc sin x ⇒du = (dx/( (√(1−x^2 )))))),((dv = dx →v = x)) :} I= [ x arcsin (x)]_0 ^(1/2) −∫^(1/2) _0 ((x dx)/( (√(1−x^2 )))) I= (1/2).(π/6)+(1/2)∫_0 ^(1/2) ((d(1−x^2 ))/( (√(1−x^2 )))) I=(π/(12))+[ (√(1−x^2 )) ]_0 ^(1/2) I=(π/(12)) + (((√3)/2)−1) = ((π+6(√3)−12)/(12))](https://www.tinkutara.com/question/Q109498.png)
$$\left(\mathrm{2}\right)\:{by}\:{part}\:\begin{cases}{{u}=\mathrm{arc}\:\mathrm{sin}\:{x}\:\Rightarrow{du}\:=\:\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}}\\{{dv}\:=\:{dx}\:\rightarrow{v}\:=\:{x}}\end{cases} \\ $$$${I}=\:\left[\:{x}\:\mathrm{arcsin}\:\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}/\mathrm{2}} \:−\underset{\mathrm{0}} {\int}^{\mathrm{1}/\mathrm{2}} \frac{{x}\:{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{2}}\overset{\mathrm{1}/\mathrm{2}} {\int}_{\mathrm{0}} \frac{{d}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${I}=\frac{\pi}{\mathrm{12}}+\left[\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\right]_{\mathrm{0}} ^{\mathrm{1}/\mathrm{2}} \\ $$$${I}=\frac{\pi}{\mathrm{12}}\:+\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{1}\right)\:=\:\frac{\pi+\mathrm{6}\sqrt{\mathrm{3}}−\mathrm{12}}{\mathrm{12}} \\ $$
Answered by 1549442205PVT last updated on 24/Aug/20
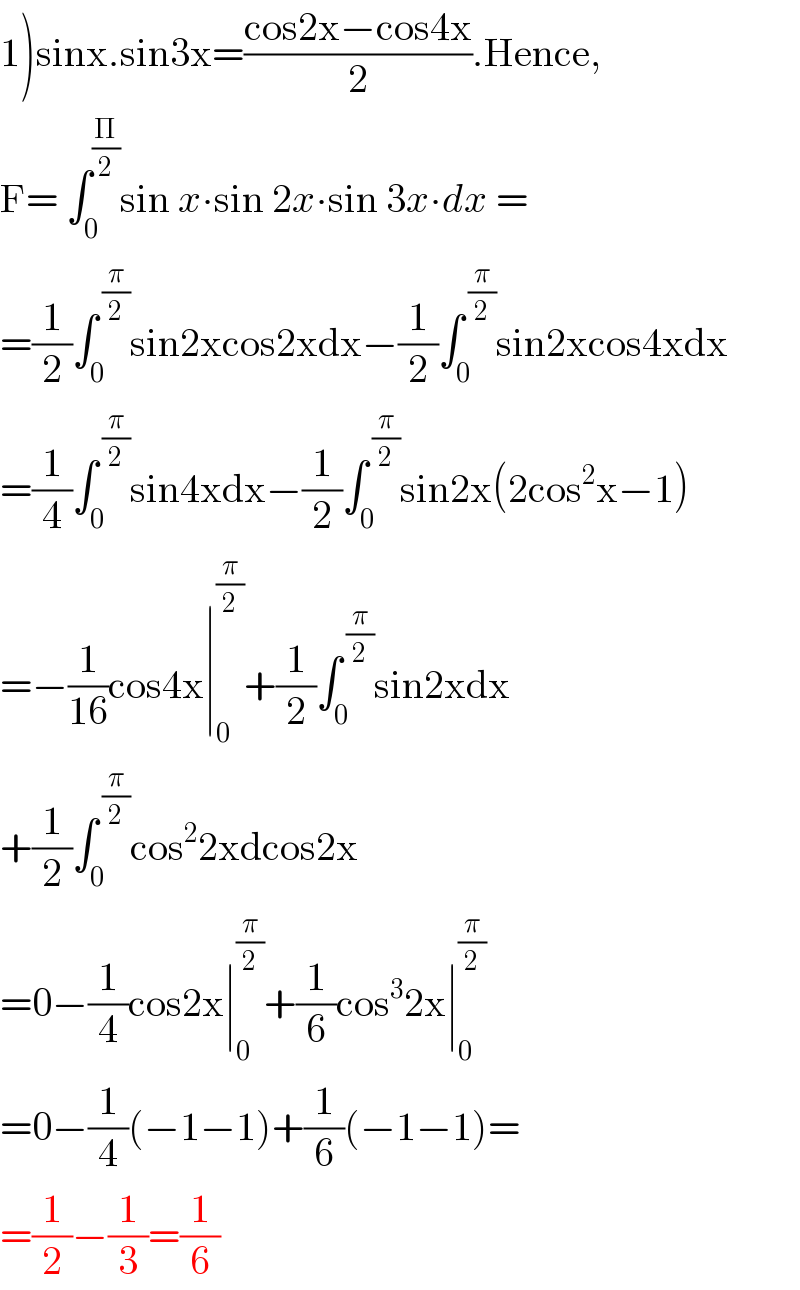
$$\left.\mathrm{1}\right)\mathrm{sinx}.\mathrm{sin3x}=\frac{\mathrm{cos2x}−\mathrm{cos4x}}{\mathrm{2}}.\mathrm{Hence}, \\ $$$$\mathrm{F}=\:\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \mathrm{sin}\:{x}\centerdot\mathrm{sin}\:\mathrm{2}{x}\centerdot\mathrm{sin}\:\mathrm{3}{x}\centerdot{dx}\:=\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{sin2xcos2xdx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{sin2xcos4xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{sin4xdx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{sin2x}\left(\mathrm{2cos}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{16}}\mathrm{cos4x}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} +\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{sin2xdx} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2}} \mathrm{2xdcos2x} \\ $$$$=\mathrm{0}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos2x}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} +\frac{\mathrm{1}}{\mathrm{6}}\mathrm{cos}^{\mathrm{3}} \mathrm{2x}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\mathrm{0}−\frac{\mathrm{1}}{\mathrm{4}}\left(−\mathrm{1}−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{6}}\left(−\mathrm{1}−\mathrm{1}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Answered by mathmax by abdo last updated on 24/Aug/20
![2) I =∫_0 ^(1/2) arcsinx dx we do the chsngement arcsinx =t ⇒x=sint ⇒ I =∫_0 ^(π/6) t cost dt =[tsint]_0 ^(π/6) −∫_0 ^(π/6) sint dt I =(π/6).(1/2) +[cost]_0 ^(π/6) =(π/(12)) +(((√3)/2)−1) ⇒I =(π/(12)) +((√3)/2)−1](https://www.tinkutara.com/question/Q109624.png)
$$\left.\mathrm{2}\right)\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{arcsinx}\:\mathrm{dx}\:\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{chsngement}\:\mathrm{arcsinx}\:=\mathrm{t}\:\Rightarrow\mathrm{x}=\mathrm{sint} \\ $$$$\Rightarrow\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\mathrm{t}\:\mathrm{cost}\:\mathrm{dt}\:=\left[\mathrm{tsint}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} −\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \mathrm{sint}\:\mathrm{dt} \\ $$$$\mathrm{I}\:=\frac{\pi}{\mathrm{6}}.\frac{\mathrm{1}}{\mathrm{2}}\:+\left[\mathrm{cost}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:=\frac{\pi}{\mathrm{12}}\:+\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{1}\right)\:\Rightarrow\mathrm{I}\:=\frac{\pi}{\mathrm{12}}\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{1} \\ $$
