Question Number 186051 by Tom last updated on 31/Jan/23
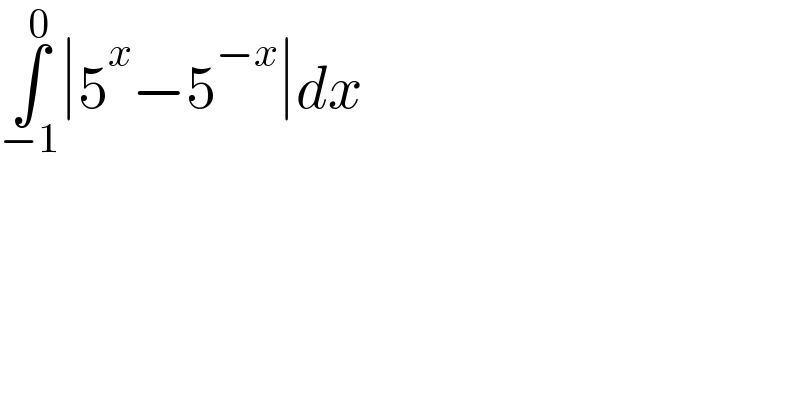
$$\underset{−\mathrm{1}} {\overset{\mathrm{0}} {\int}}\mid\mathrm{5}^{{x}} −\mathrm{5}^{−{x}} \mid{dx} \\ $$
Answered by Frix last updated on 31/Jan/23
![=∫_(−1) ^0 ∣2sinh (xln 5)∣dx= =−2∫_(−1) ^0 sinh (xln 5) dx= =−(2/(ln 5))[cosh (xln 5)]_(−1) ^0 =((16)/(5ln 5))](https://www.tinkutara.com/question/Q186055.png)
$$=\underset{−\mathrm{1}} {\overset{\mathrm{0}} {\int}}\mid\mathrm{2sinh}\:\left({x}\mathrm{ln}\:\mathrm{5}\right)\mid{dx}= \\ $$$$=−\mathrm{2}\underset{−\mathrm{1}} {\overset{\mathrm{0}} {\int}}\mathrm{sinh}\:\left({x}\mathrm{ln}\:\mathrm{5}\right)\:{dx}= \\ $$$$=−\frac{\mathrm{2}}{\mathrm{ln}\:\mathrm{5}}\left[\mathrm{cosh}\:\left({x}\mathrm{ln}\:\mathrm{5}\right)\right]_{−\mathrm{1}} ^{\mathrm{0}} =\frac{\mathrm{16}}{\mathrm{5ln}\:\mathrm{5}} \\ $$
