Question Number 181735 by Mastermind last updated on 29/Nov/22
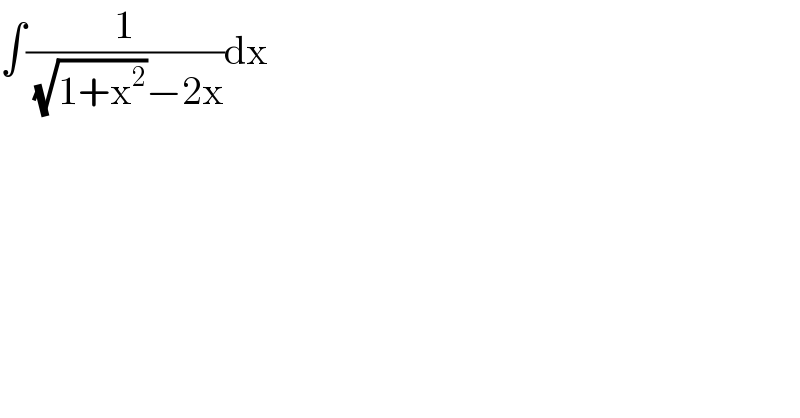
$$\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }−\mathrm{2x}}\mathrm{dx} \\ $$
Answered by Gamil last updated on 29/Nov/22

Answered by MJS_new last updated on 30/Nov/22
![∫(dx/(−2x+(√(x^2 +1))))= [t=x+(√(x^2 +1)) → dx=((t^2 +1)/(2t^2 ))dt] =−∫((t^2 +1)/(t(t^2 −3)))dt= =∫((1/(3t))−(2/(3(t−(√3))))−(2/(3(t+(√3)))))dt= =(1/3)ln t −(2/3)(ln (t−(√3)) +ln (t+(√3)))= =(1/3)ln (t/((t^2 −3)^2 )) = =(1/3)ln ((x^2 +1)^(3/2) −x(x^2 −3)) −(2/3)ln ∣3x^2 −1∣ +C](https://www.tinkutara.com/question/Q181802.png)
$$\int\frac{{dx}}{−\mathrm{2}{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dx}=\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }{dt}\right] \\ $$$$=−\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}\left({t}^{\mathrm{2}} −\mathrm{3}\right)}{dt}= \\ $$$$=\int\left(\frac{\mathrm{1}}{\mathrm{3}{t}}−\frac{\mathrm{2}}{\mathrm{3}\left({t}−\sqrt{\mathrm{3}}\right)}−\frac{\mathrm{2}}{\mathrm{3}\left({t}+\sqrt{\mathrm{3}}\right)}\right){dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:{t}\:−\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{ln}\:\left({t}−\sqrt{\mathrm{3}}\right)\:+\mathrm{ln}\:\left({t}+\sqrt{\mathrm{3}}\right)\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\frac{{t}}{\left({t}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} }\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\left(\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} −{x}\left({x}^{\mathrm{2}} −\mathrm{3}\right)\right)\:−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\:\mid\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\mid\:+{C} \\ $$
