Question Number 88357 by jagoll last updated on 10/Apr/20
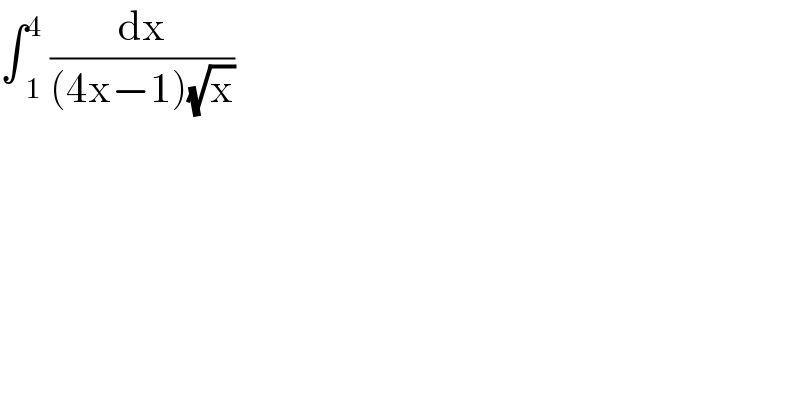
$$\int\underset{\mathrm{1}} {\overset{\mathrm{4}} {\:}}\:\frac{\mathrm{dx}}{\left(\mathrm{4x}−\mathrm{1}\right)\sqrt{\mathrm{x}}} \\ $$
Commented by john santu last updated on 10/Apr/20
![[ t=(√x) , 2t dt = dx ] ∫_1 ^2 ((2t dt )/((4t^2 −1)t)) = ∫ _1 ^( 2) ((2 dt)/((2t−1)(2t+1))) = ∫_1 ^2 (dt/(2t−1)) −∫ _1 ^( 2) (dt/(2t+1)) = (1/2) ln ∣((2t−1)/(2t+1))∣_( 1) ^( 2) = (1/2){ ln((3/5))−ln((1/3))} = (1/2)ln ((9/5))](https://www.tinkutara.com/question/Q88358.png)
$$\left[\:{t}=\sqrt{{x}}\:,\:\mathrm{2}{t}\:{dt}\:=\:{dx}\:\right]\: \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:\frac{\mathrm{2}{t}\:{dt}\:}{\left(\mathrm{4}{t}^{\mathrm{2}} −\mathrm{1}\right){t}}\:=\:\int\overset{\:\:\mathrm{2}} {\:}_{\mathrm{1}} \frac{\mathrm{2}\:{dt}}{\left(\mathrm{2}{t}−\mathrm{1}\right)\left(\mathrm{2}{t}+\mathrm{1}\right)} \\ $$$$=\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{{dt}}{\mathrm{2}{t}−\mathrm{1}}\:−\int\underset{\mathrm{1}} {\overset{\:\mathrm{2}} {\:}}\:\frac{{dt}}{\mathrm{2}{t}+\mathrm{1}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\:\mid\frac{\mathrm{2}{t}−\mathrm{1}}{\mathrm{2}{t}+\mathrm{1}}\underset{\:\:\mathrm{1}} {\overset{\:\:\mathrm{2}} {\mid}}=\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{5}}\right)−\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right\} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\frac{\mathrm{9}}{\mathrm{5}}\right) \\ $$
