Question Number 57225 by maxmathsup by imad last updated on 31/Mar/19
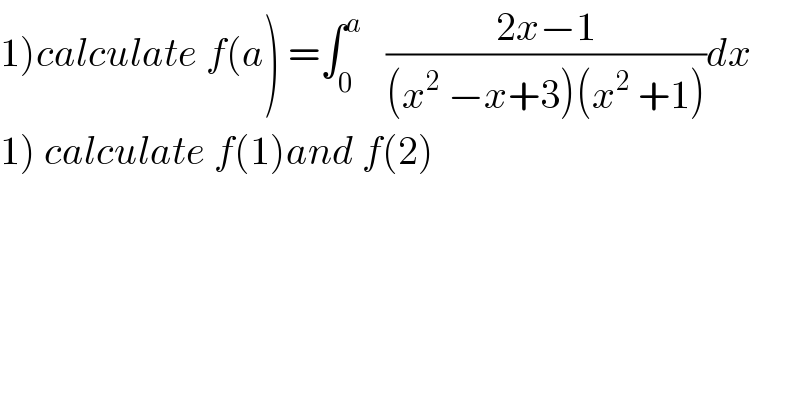
$$\left.\mathrm{1}\right){calculate}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{{a}} \:\:\:\frac{\mathrm{2}{x}−\mathrm{1}}{\left({x}^{\mathrm{2}} \:−{x}+\mathrm{3}\right)\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}{dx} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}\left(\mathrm{1}\right){and}\:{f}\left(\mathrm{2}\right) \\ $$
Commented by maxmathsup by imad last updated on 04/Apr/19
![let decompose F(x) =((2x−1)/((x^2 −x+3)(x^2 +1))) ⇒ F(x) =((ax+b)/(x^2 −x+3)) +((cx+d)/(x^2 +1)) ⇒(ax+b)(x^2 +1)+(cx+d)(x^2 −x+3) =2x−1 ⇒ ax^3 +ax +bx^2 +b +cx^3 −cx^2 +3cx +dx^2 −dx +3d =2x−1 ⇒ (a+c)x^3 +(b−c +d)x^2 +(a +3c−d)x +b +3d =2x−1 ⇒ a+c =0 and b−c+d =0 and a+3c−d =2 and 3d=−1 ⇒ d =−(1/3) c=−a ⇒a−3a −d =2 ⇒−2a =d+2 =−(1/3) +2 =(5/3) ⇒a =−(5/6) c =(5/6) ,b =c−d =(5/6) +(1/3) =(7/6) ⇒ F(x) =((−(5/6)x +(7/6))/(x^2 −x+3)) +(((5/6)x−(2/6))/(x^2 +1)) =−(1/6) ((x−7)/(x^2 −x+3)) +(1/6) ((5x−2)/(x^2 +1)) ⇒ ∫ F(x)dx =−(1/(12)) ∫ ((2x−14)/(x^2 −x +3))dx +(5/(12)) ∫ ((2x)/(x^2 +1)) −(1/3) ∫ (dx/(x^2 +1)) =−(1/(12))ln(x^2 −x +3) +((13)/(12)) ∫ (dx/(x^2 −x +3)) +(5/(12))ln(x^2 +1)−(1/3) arctan(x) +c but ∫ (dx/(x^2 −x+3)) =∫ (dx/(x^2 −2(x/2) +(1/4)+3−(1/4))) =∫ (dx/((x−(1/2))^2 +((11)/4))) =_(x−(1/2)=((√(11))/2)u) (4/(11))∫ (1/(1+u^2 )) ((√(11))/2) du =(2/( (√(11)))) arctan(((2x−1)/( (√(11))))) ⇒ ∫ F(x)dx =−(1/(12))ln(x^2 −x+3) +((13)/(6(√(11)))) arctan(((2x−1)/( (√(11))))) +(5/(12))ln(x^2 +1)−(1/3)arctan(x)+c ⇒f(a) =∫_0 ^a F(x)dx =[−(1/(12))ln(x^2 −x+3)+((13)/(6(√(11)))) arctan(((2x−1)/( (√(11)))))+(5/(12))ln(x^2 +1)−(1/3) arctan(x)]_0 ^a =−(1/(12))ln(a^2 −a +3)+((13)/(6(√(11)))) arctan(((2a−1)/( (√(11)))))+(5/(12))ln(a^2 +1)−(1/3) arctan(a) +(1/(12))ln(3) +((13)/(6(√(11)))) arctan((1/( (√(11)))))](https://www.tinkutara.com/question/Q57467.png)
$${let}\:{decompose}\:{F}\left({x}\right)\:=\frac{\mathrm{2}{x}−\mathrm{1}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{{ax}+{b}}{{x}^{\mathrm{2}} −{x}+\mathrm{3}}\:+\frac{{cx}+{d}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\left({ax}+{b}\right)\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)+\left({cx}+{d}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)\:=\mathrm{2}{x}−\mathrm{1}\:\Rightarrow \\ $$$${ax}^{\mathrm{3}} \:+{ax}\:+{bx}^{\mathrm{2}} \:+{b}\:+{cx}^{\mathrm{3}} \:−{cx}^{\mathrm{2}} \:+\mathrm{3}{cx}\:+{dx}^{\mathrm{2}} \:−{dx}\:+\mathrm{3}{d}\:=\mathrm{2}{x}−\mathrm{1}\:\Rightarrow \\ $$$$\left({a}+{c}\right){x}^{\mathrm{3}} \:+\left({b}−{c}\:+{d}\right){x}^{\mathrm{2}} \:+\left({a}\:+\mathrm{3}{c}−{d}\right){x}\:+{b}\:+\mathrm{3}{d}\:=\mathrm{2}{x}−\mathrm{1}\:\Rightarrow \\ $$$${a}+{c}\:=\mathrm{0}\:{and}\:{b}−{c}+{d}\:=\mathrm{0}\:{and}\:{a}+\mathrm{3}{c}−{d}\:=\mathrm{2}\:{and}\:\mathrm{3}{d}=−\mathrm{1}\:\Rightarrow\:{d}\:=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${c}=−{a}\:\Rightarrow{a}−\mathrm{3}{a}\:−{d}\:=\mathrm{2}\:\Rightarrow−\mathrm{2}{a}\:={d}+\mathrm{2}\:=−\frac{\mathrm{1}}{\mathrm{3}}\:+\mathrm{2}\:=\frac{\mathrm{5}}{\mathrm{3}}\:\Rightarrow{a}\:=−\frac{\mathrm{5}}{\mathrm{6}} \\ $$$${c}\:=\frac{\mathrm{5}}{\mathrm{6}}\:\:,{b}\:={c}−{d}\:=\frac{\mathrm{5}}{\mathrm{6}}\:+\frac{\mathrm{1}}{\mathrm{3}}\:=\frac{\mathrm{7}}{\mathrm{6}}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{−\frac{\mathrm{5}}{\mathrm{6}}{x}\:+\frac{\mathrm{7}}{\mathrm{6}}}{{x}^{\mathrm{2}} −{x}+\mathrm{3}}\:+\frac{\frac{\mathrm{5}}{\mathrm{6}}{x}−\frac{\mathrm{2}}{\mathrm{6}}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:=−\frac{\mathrm{1}}{\mathrm{6}}\:\frac{{x}−\mathrm{7}}{{x}^{\mathrm{2}} −{x}+\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{6}}\:\frac{\mathrm{5}{x}−\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:{F}\left({x}\right){dx}\:=−\frac{\mathrm{1}}{\mathrm{12}}\:\int\:\frac{\mathrm{2}{x}−\mathrm{14}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{3}}{dx}\:\:+\frac{\mathrm{5}}{\mathrm{12}}\:\int\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{3}}\:\int\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{12}}{ln}\left({x}^{\mathrm{2}} −{x}\:+\mathrm{3}\right)\:+\frac{\mathrm{13}}{\mathrm{12}}\:\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{3}}\:+\frac{\mathrm{5}}{\mathrm{12}}{ln}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{3}}\:{arctan}\left({x}\right)\:+{c} \\ $$$${but}\:\int\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{3}}\:=\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}\frac{{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{3}−\frac{\mathrm{1}}{\mathrm{4}}}\:=\int\:\:\:\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{11}}{\mathrm{4}}} \\ $$$$=_{{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}{u}} \:\:\:\frac{\mathrm{4}}{\mathrm{11}}\int\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\:{du}\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{11}}}\:{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{11}}}\right)\:\Rightarrow \\ $$$$\int\:{F}\left({x}\right){dx}\:=−\frac{\mathrm{1}}{\mathrm{12}}{ln}\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)\:+\frac{\mathrm{13}}{\mathrm{6}\sqrt{\mathrm{11}}}\:{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{11}}}\right)\:+\frac{\mathrm{5}}{\mathrm{12}}{ln}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{3}}{arctan}\left({x}\right)+{c}\: \\ $$$$\Rightarrow{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{{a}} \:{F}\left({x}\right){dx}\:=\left[−\frac{\mathrm{1}}{\mathrm{12}}{ln}\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)+\frac{\mathrm{13}}{\mathrm{6}\sqrt{\mathrm{11}}}\:{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{11}}}\right)+\frac{\mathrm{5}}{\mathrm{12}}{ln}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{3}}\:{arctan}\left({x}\right)\right]_{\mathrm{0}} ^{{a}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{12}}{ln}\left({a}^{\mathrm{2}} −{a}\:+\mathrm{3}\right)+\frac{\mathrm{13}}{\mathrm{6}\sqrt{\mathrm{11}}}\:{arctan}\left(\frac{\mathrm{2}{a}−\mathrm{1}}{\:\sqrt{\mathrm{11}}}\right)+\frac{\mathrm{5}}{\mathrm{12}}{ln}\left({a}^{\mathrm{2}} \:+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{3}}\:{arctan}\left({a}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{12}}{ln}\left(\mathrm{3}\right)\:+\frac{\mathrm{13}}{\mathrm{6}\sqrt{\mathrm{11}}}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{11}}}\right) \\ $$
Commented by maxmathsup by imad last updated on 05/Apr/19
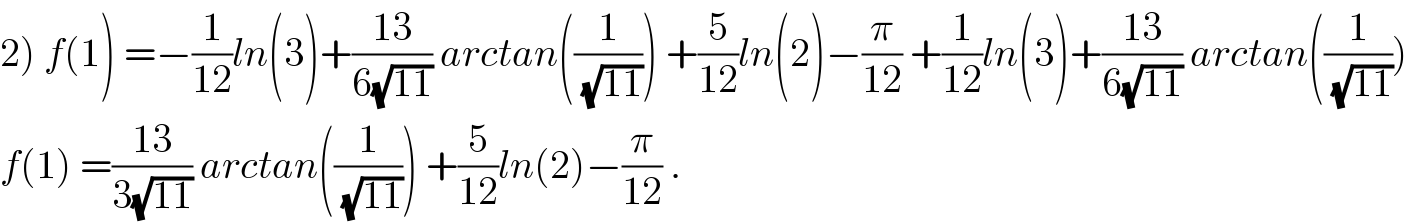
$$\left.\mathrm{2}\right)\:{f}\left(\mathrm{1}\right)\:=−\frac{\mathrm{1}}{\mathrm{12}}{ln}\left(\mathrm{3}\right)+\frac{\mathrm{13}}{\mathrm{6}\sqrt{\mathrm{11}}}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{11}}}\right)\:+\frac{\mathrm{5}}{\mathrm{12}}{ln}\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{12}}\:+\frac{\mathrm{1}}{\mathrm{12}}{ln}\left(\mathrm{3}\right)+\frac{\mathrm{13}}{\mathrm{6}\sqrt{\mathrm{11}}}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{11}}}\right) \\ $$$${f}\left(\mathrm{1}\right)\:=\frac{\mathrm{13}}{\mathrm{3}\sqrt{\mathrm{11}}}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{11}}}\right)\:+\frac{\mathrm{5}}{\mathrm{12}}{ln}\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{12}}\:. \\ $$
