1-i-2-i-2-i-1-i-3-500x-500yi-find-x-y-

Question Number 80890 by M±th+et£s last updated on 07/Feb/20

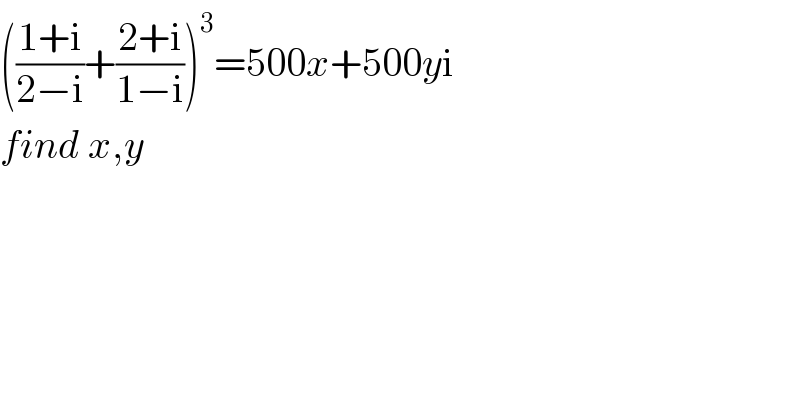
$$\left(\frac{\mathrm{1}+\mathrm{i}}{\mathrm{2}−\mathrm{i}}+\frac{\mathrm{2}+\mathrm{i}}{\mathrm{1}−\mathrm{i}}\right)^{\mathrm{3}} =\mathrm{500}{x}+\mathrm{500}{y}\mathrm{i} \\ $$$${find}\:{x},{y} \\ $$

Answered by behi83417@gmail.com last updated on 07/Feb/20

$$\frac{\left(\mathrm{1}+\mathrm{i}\right)\left(\mathrm{2}+\mathrm{i}\right)}{\mathrm{2}+\mathrm{1}}=\frac{\mathrm{2}+\mathrm{i}+\mathrm{2i}+\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{3}+\mathrm{3i}}{\mathrm{3}}=\mathrm{1}+\mathrm{i} \\ $$$$\frac{\mathrm{2}+\mathrm{i}}{\mathrm{1}−\mathrm{i}}=\frac{\left(\mathrm{2}+\mathrm{i}\right)\left(\mathrm{1}+\mathrm{i}\right)}{\mathrm{1}+\mathrm{1}}=\frac{\mathrm{2}+\mathrm{2i}+\mathrm{i}+\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}+\mathrm{3i}}{\mathrm{2}} \\ $$$$\mathrm{LHS}=\left[\mathrm{1}+\mathrm{i}+\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{i}\right)\right]^{\mathrm{3}} =\left[\frac{\mathrm{5}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{i}\right)\right]^{\mathrm{3}} = \\ $$$$=\frac{\mathrm{125}}{\mathrm{8}}\left(\mathrm{1}+\mathrm{3i}+\mathrm{3i}^{\mathrm{2}} +\mathrm{i}^{\mathrm{3}} \right)=\frac{\mathrm{125}}{\mathrm{8}}\left(\mathrm{1}+\mathrm{3i}−\mathrm{3}−\mathrm{i}\right)= \\ $$$$=\frac{\mathrm{125}}{\mathrm{8}}\left(\mathrm{2i}−\mathrm{2}\right)=\frac{\mathrm{125}}{\mathrm{4}}\left(\mathrm{i}−\mathrm{1}\right)=\mathrm{500x}+\mathrm{500yi} \\ $$$$\Rightarrow\mathrm{i}−\mathrm{1}=\mathrm{16x}+\mathrm{16yi}\Rightarrow\begin{cases}{\mathrm{x}=\frac{−\mathrm{1}}{\mathrm{16}}}\\{\mathrm{y}=\frac{\mathrm{1}}{\mathrm{16}}}\end{cases}\:\:\:. \\ $$

Commented by M±th+et£s last updated on 07/Feb/20

$${thank}\:{you}\:{sir} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com