Question Number 89255 by M±th+et£s last updated on 16/Apr/20
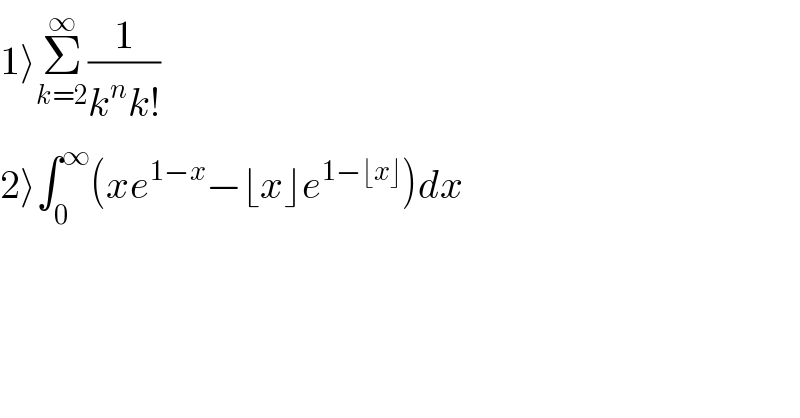
$$\mathrm{1}\rangle\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{{n}} {k}!} \\ $$$$\mathrm{2}\rangle\int_{\mathrm{0}} ^{\infty} \left({xe}^{\mathrm{1}−{x}} −\lfloor{x}\rfloor{e}^{\mathrm{1}−\lfloor{x}\rfloor} \right){dx} \\ $$
Commented by mathmax by abdo last updated on 16/Apr/20
![2) I =∫_0 ^∞ (x e^(1−x) −[x]e^(1−[x]) )dx =∫_0 ^∞ xe^(1−x) dx−∫_0 ^∞ [x]e^(1−[x]) dx we have ∫_0 ^∞ x e^(1−x) dx =_(by parts) [−x e^(1−x) ]_0 ^(+∞) +∫_0 ^∞ e^(1−x) dx =[−e^(1−x) ]_0 ^(+∞) =e ∫_0 ^∞ [x]e^(1−[x]) dx =Σ_(n=0) ^∞ ∫_n ^(n+1) n e^(1−n) dx =Σ_(n=0) ^∞ ne^(1−n) =e Σ_(n=0) ^∞ n((1/e))^n =ew((1/e)) with w(x)Σ_(n=0) ^∞ nx^n ∣x∣<1 we have Σ_(n=0) ^∞ x^n =(1/(1−x)) ⇒Σ_(n=1) ^∞ nx^(n−1) =(1/((1−x)^2 )) ⇒ Σ_(n=1) ^∞ nx^n =(x/((1−x)^2 )) ⇒Σ_(n=1) ^∞ n((1/e))^n =(1/(e(1−(1/e))^2 )) =(1/(e(((e−1)/e))^2 )) =(e/((e−1)^2 )) ⇒∫_0 ^∞ [x]e^(1−[x]) dx =(e^2 /((e−1)^2 )) ⇒ ∫_0 ^∞ (xe^(1−x) −[x]e^(1−[x]) )dx =e−(e^2 /((e−1)^2 ))](https://www.tinkutara.com/question/Q89278.png)
$$\left.\mathrm{2}\right)\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\left({x}\:{e}^{\mathrm{1}−{x}} −\left[{x}\right]{e}^{\mathrm{1}−\left[{x}\right]} \right){dx}\:=\int_{\mathrm{0}} ^{\infty} \:{xe}^{\mathrm{1}−{x}} \:{dx}−\int_{\mathrm{0}} ^{\infty} \left[{x}\right]{e}^{\mathrm{1}−\left[{x}\right]} {dx} \\ $$$${we}\:{have}\:\int_{\mathrm{0}} ^{\infty} \:{x}\:{e}^{\mathrm{1}−{x}} \:{dx}\:=_{{by}\:{parts}} \left[−{x}\:{e}^{\mathrm{1}−{x}} \right]_{\mathrm{0}} ^{+\infty} +\int_{\mathrm{0}} ^{\infty} \:{e}^{\mathrm{1}−{x}} \:{dx} \\ $$$$=\left[−{e}^{\mathrm{1}−{x}} \right]_{\mathrm{0}} ^{+\infty} \:={e} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\left[{x}\right]{e}^{\mathrm{1}−\left[{x}\right]} \:{dx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\int_{{n}} ^{{n}+\mathrm{1}} \:{n}\:{e}^{\mathrm{1}−{n}} \:{dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:{ne}^{\mathrm{1}−{n}} \:={e}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{n}\left(\frac{\mathrm{1}}{{e}}\right)^{{n}} \:={ew}\left(\frac{\mathrm{1}}{{e}}\right)\:{with}\:{w}\left({x}\right)\sum_{{n}=\mathrm{0}} ^{\infty} \:{nx}^{{n}} \\ $$$$\mid{x}\mid<\mathrm{1}\:\:{we}\:{have}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}−\mathrm{1}} \:=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}} \:=\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:{n}\left(\frac{\mathrm{1}}{{e}}\right)^{{n}} \:=\frac{\mathrm{1}}{{e}\left(\mathrm{1}−\frac{\mathrm{1}}{{e}}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{{e}\left(\frac{{e}−\mathrm{1}}{{e}}\right)^{\mathrm{2}} } \\ $$$$=\frac{{e}}{\left({e}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\left[{x}\right]{e}^{\mathrm{1}−\left[{x}\right]} {dx}\:=\frac{{e}^{\mathrm{2}} }{\left({e}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \left({xe}^{\mathrm{1}−{x}} −\left[{x}\right]{e}^{\mathrm{1}−\left[{x}\right]} \right){dx}\:={e}−\frac{{e}^{\mathrm{2}} }{\left({e}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by M±th+et£s last updated on 16/Apr/20

$${thank}\:{you}\:{sir} \\ $$
Commented by M±th+et£s last updated on 16/Apr/20

$${there}\:{is}\:{a}\:{typo} \\ $$$${Q}_{\mathrm{1}} /{show}\:{that}\:\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{{x}^{{k}} }{{k}^{{n}} {k}!}={e}^{{x}} −\mathrm{1} \\ $$
