Question Number 49134 by AdqhK ÐQeQqQ last updated on 03/Dec/18
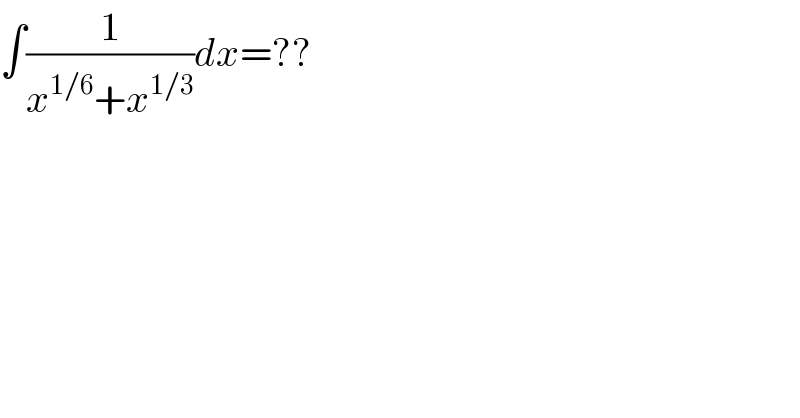
$$\int\frac{\mathrm{1}}{{x}^{\mathrm{1}/\mathrm{6}} +{x}^{\mathrm{1}/\mathrm{3}} }{dx}=?? \\ $$
Answered by arvinddayama01@gmail.com. last updated on 03/Dec/18
![put x=t^6 dx=6t^5 dt 6∫(t^5 /(1+t^2 ))dt 6∫[t^3 −t+(t/(1+t^2 ))] 6∫t^3 dt−6∫tdt+3∫((2t)/(1+t^2 ))dt (6/4)t^4 −(6/2)t^2 +3ln(1+t^2 )+C (3/2)t^4 −3t^2 +3ln(1+t^2 )+C t = x^(1/6) value put then (3/2)x^(2/3) −3t^(1/3) +3ln(1+x^(1/3) )+C](https://www.tinkutara.com/question/Q49137.png)
$${put}\:\:{x}={t}^{\mathrm{6}} \\ $$$$\:\:\:\:\:\:\:{dx}=\mathrm{6}{t}^{\mathrm{5}} {dt} \\ $$$$\mathrm{6}\int\frac{{t}^{\mathrm{5}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\mathrm{6}\int\left[{t}^{\mathrm{3}} −{t}+\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right] \\ $$$$\mathrm{6}\int{t}^{\mathrm{3}} {dt}−\mathrm{6}\int{tdt}+\mathrm{3}\int\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\frac{\mathrm{6}}{\mathrm{4}}{t}^{\mathrm{4}} −\frac{\mathrm{6}}{\mathrm{2}}{t}^{\mathrm{2}} +\mathrm{3}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+{C} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}{t}^{\mathrm{4}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{3}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+{C} \\ $$$${t}\:=\:{x}^{\mathrm{1}/\mathrm{6}} \:{value}\:{put}\:{then} \\ $$$$\:\:\:\:\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}/\mathrm{3}} −\mathrm{3}{t}^{\mathrm{1}/\mathrm{3}} +\mathrm{3}{ln}\left(\mathrm{1}+{x}^{\mathrm{1}/\mathrm{3}} \right)+{C} \\ $$
Commented by AdqhK ÐQeQqQ last updated on 03/Dec/18

$${thanku}\:{sir} \\ $$
Commented by arvinddayama01@gmail.com. last updated on 03/Dec/18

$${your}\:{welcome} \\ $$
