Question Number 54586 by arvinddayama00@gmail.com last updated on 07/Feb/19
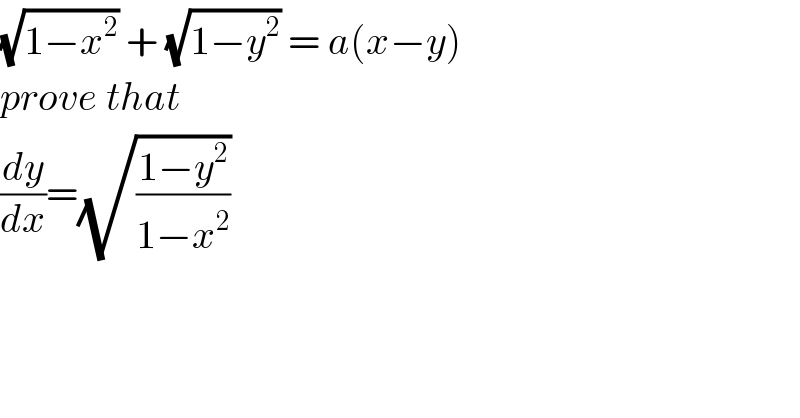
$$\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+\:\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\:=\:{a}\left({x}−{y}\right) \\ $$$${prove}\:{that} \\ $$$$\frac{{dy}}{{dx}}=\sqrt{\frac{\mathrm{1}−{y}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Feb/19
![x=sinp y=sinq (dx/dp)=cosp (dy/dq)=cosq (dy/dx)=((cosqdq)/(cospdp)) (√(1−x^2 )) +(√(1−y^2 )) =a(x−y) cosp+cosq=a(sinp−sinq) a=((2cos((p+q)/2)×cos((p−q)/2))/(2cos((p+q)/2)sin((p−q)/2))) tan((p−q)/2)=(1/a) sec^2 (((p−q)/2))((((dp/dx)−(dq/(dx )))/2))=0 so (dp/dx)−(dq/dx)=0 so (dp/dq)=1 now(dy/dx)=((cosq)/(cosp))×(dq/dp)[(dq/dp)=1] (dy/dx)=((cosq)/(cosp))=((√(1−y^2 ))/( (√(1−x^2 ))))](https://www.tinkutara.com/question/Q54590.png)
$${x}={sinp}\:\:{y}={sinq} \\ $$$$\frac{{dx}}{{dp}}={cosp}\:\:\:\frac{{dy}}{{dq}}={cosq} \\ $$$$\frac{{dy}}{{dx}}=\frac{{cosqdq}}{{cospdp}} \\ $$$$\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\:={a}\left({x}−{y}\right) \\ $$$${cosp}+{cosq}={a}\left({sinp}−{sinq}\right) \\ $$$${a}=\frac{\mathrm{2}{cos}\frac{{p}+{q}}{\mathrm{2}}×{cos}\frac{{p}−{q}}{\mathrm{2}}}{\mathrm{2}{cos}\frac{{p}+{q}}{\mathrm{2}}{sin}\frac{{p}−{q}}{\mathrm{2}}} \\ $$$${tan}\frac{{p}−{q}}{\mathrm{2}}=\frac{\mathrm{1}}{{a}} \\ $$$${sec}^{\mathrm{2}} \left(\frac{{p}−{q}}{\mathrm{2}}\right)\left(\frac{\frac{{dp}}{{dx}}−\frac{{dq}}{{dx}\:}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$${so}\:\frac{{dp}}{{dx}}−\frac{{dq}}{{dx}}=\mathrm{0}\:\:{so}\:\frac{{dp}}{{dq}}=\mathrm{1} \\ $$$${now}\frac{{dy}}{{dx}}=\frac{{cosq}}{{cosp}}×\frac{{dq}}{{dp}}\left[\frac{{dq}}{{dp}}=\mathrm{1}\right] \\ $$$$\frac{{dy}}{{dx}}=\frac{{cosq}}{{cosp}}=\frac{\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} \:}} \\ $$
Commented by arvinddayama00@gmail.com last updated on 08/Feb/19

$${any}\:{or}\:{solution}\: \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 08/Feb/19
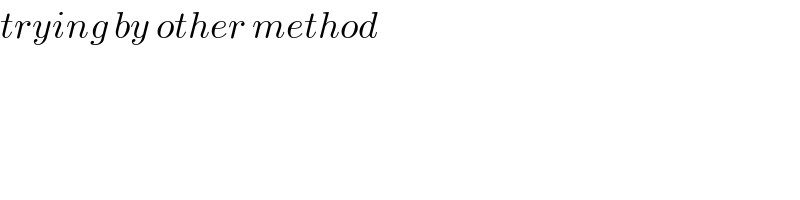
$${trying}\:{by}\:{other}\:{method} \\ $$
